题目内容
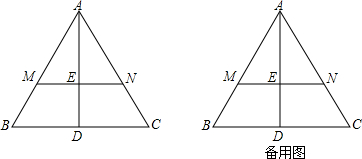
8.如图,△ABC是边长为6的等边三角形,AD⊥BC于点D,点M是AB边上的点,且BM=$\frac{1}{3}$AB,过点M作MN∥BC交AD于点E,交AC于点N.(1)求ME的长;
(2)将图中的△AMN以每秒1个单位长度的速度沿线段AB从点A向点B平移,当点A与点B重合时停止移动,△AMN运动的时间为t秒,△AMN与四边形BDEM重叠部分的面积为s,请直接写出s与t之间的函数关系式,并写出相应t的取值范围;
(3)将图中的△AMN绕点E逆时针旋转,设直线AE与直线BC交于点O.在△AMN旋转过程中,是否存在这样的点O,使△BOE为等腰三角形?若存在,请求出此时△AMN绕E逆时针旋转的旋转角α的大小(0°<α≤180°);若不存在,请说明理由.
分析 (1)由等边三角形的性质得到三角形的高,再根据三角形相似得到比例式求出AM,代入含30°的直角三角形中计算即可;
(2)分三种情况讨论,根据三角形相似,计算出相应图形的底和高,代入相应图形的面积公式即可得到结果;
(3)当△AMN绕点O①顺时针旋转15°,②顺时针旋转60°,③逆时针旋转30°,④逆时针旋转75°时,△CPQ为等腰三角形.
解答 解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
又∵AD⊥BC,
∴$∠MAE=\frac{1}{2}∠BAC=30°$,
∴MN∥BC,AD⊥BC,
∴∠AEM=∠ADB=90°,
∴$ME=\frac{1}{2}AM$.
∵△ABC的边长为6,BM=$\frac{1}{3}$AB,
∴BM=2,
∴AM=AB-BM=6-2=4,
∴ME=2;
(2)$s=\frac{{\sqrt{3}}}{8}{t^2}+\sqrt{3}t$(0≤t≤2);
$s=-\frac{{\sqrt{3}}}{2}{t^2}+2\sqrt{3}t+\frac{{\sqrt{3}}}{2}$(2<t≤3);
$s=-\sqrt{3}t+5\sqrt{3}$(3<t≤4);
$s=\frac{{\sqrt{3}}}{4}{t^2}-3\sqrt{3}t+9\sqrt{3}$(4<t≤6).
(3)由题意得:∠MEB=∠MBE=∠DBE=30°,∠BED=60°.
(ⅰ)当BE=BO,且点O在点B右边时(答图1),
∵BE=BO,
∴∠BEO=∠BOE,
∵∠EBD=30°,
∴∠BEO=75°,
∴∠DEO=15°,
∴α=15°,
当BE=BO,且点O在点B左边时(答图2),
∵OB=EB,
∴∠BOE=∠BEO=15°,
∴∠OEM=15°,
∴α=90°+15°=105°
(ⅱ)当EB=EO时(答图3),
∵EB=EO,
∴∠EBO=∠EOB=30°,
∴∠BEO=120°,
∴∠DEO=60°,
∴α=60°.
(ⅲ)当OB=OE时(答图4),
∵OB=OE,
∴∠BEO=∠EBO=30°,
∴α=90°+30°+30°=150°.
综上所述:存在这样的点O,使△BOE为等腰三角形,
此时旋转角α的大小为15°或105°或60°或150°.
点评 本题考查了图形的变换-平移,等边三角形的性质,相似三角形的判定和性质,三角形的面积的计算,注意分类讨论是解题的关键.


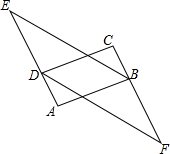 如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.
如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.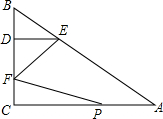 如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.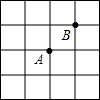 已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数有多少?并在图中标出C点的位置.
已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数有多少?并在图中标出C点的位置.