题目内容
 如图,厂房屋顶人字架(等腰三角形)的跨度为10,∠B=36°,求中柱AD(D为底边中点)和上弦AB的长(结果保留小数点后两位).
如图,厂房屋顶人字架(等腰三角形)的跨度为10,∠B=36°,求中柱AD(D为底边中点)和上弦AB的长(结果保留小数点后两位).考点:解直角三角形的应用
专题:
分析:根据等腰三角形“三线合一”的性质得到BD=5,然后通过解直角△ABD来求AD、AB的长度.
解答:解:∵AB=AC,AD⊥BC,BC=10,
∴BD=
BC=5,
∴AD=BD•tan36°≈5×0.727=3.63.
AB=
≈
≈6.18.
∴BD=
| 1 |
| 2 |
∴AD=BD•tan36°≈5×0.727=3.63.
AB=
| BD |
| cos36° |
| 5 |
| 0.809 |
点评:本题考查解直角三角形的应用.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列命题:①圆的切线垂直于经过切点的半径;②掷一枚有正反面的均匀硬币,正面和反面朝上的概率都是0.5;③相等的圆心角所对的弧相等;④某种彩票的中奖率为
,佳佳买10张彩票一定能中奖.其中,正确的命题是( )
| 1 |
| 10 |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
下列命题中,正确的是( )
| A、平面上三个点确定一个圆 |
| B、等弧所对的圆周角相等 |
| C、平分弦的直径垂直于这条弦 |
| D、方程x2+x+1=0的两个实数根之积为-1 |
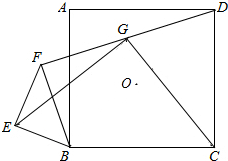 正方形ABCD中,以B为端点在正方形外作等腰直角△BEF,∠BEF=90°,连接DF,取DF的中点G,并连接EG、CG.求证:EG=CG,EG⊥CG.
正方形ABCD中,以B为端点在正方形外作等腰直角△BEF,∠BEF=90°,连接DF,取DF的中点G,并连接EG、CG.求证:EG=CG,EG⊥CG.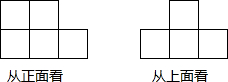 如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题:
如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题: