题目内容
【题目】对于平面内的点![]() 和点
和点![]() ,给出如下定义:点
,给出如下定义:点![]() 为平面内一点,若点
为平面内一点,若点![]() 使得
使得![]() 是以
是以![]() 为顶角且
为顶角且![]() 小于90°的等腰三角形,则称点
小于90°的等腰三角形,则称点![]() 是点
是点![]() 关于点
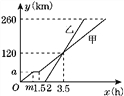
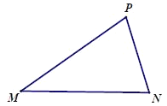
关于点![]() 的锐角等腰点.如图,点
的锐角等腰点.如图,点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.
的锐角等腰点.
在平面直角坐标系xOy中,点O为坐标原点
(1)已知点![]() ,在点
,在点![]() ,
,![]() ,
,![]() ,
,![]() 中,是点
中,是点![]() 关于点
关于点![]() 的锐角等腰点的是 ;
的锐角等腰点的是 ;
(2)已知点![]() ,点
,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点,求实数
的锐角等腰点,求实数![]() 的取值范围.
的取值范围.
(3) 点![]() 是
是![]() 轴上的动点,
轴上的动点,![]() ,
,![]() ,点
,点![]() 是以点
是以点![]() 为圆心,2为半径的圆上一动点.且满足
为圆心,2为半径的圆上一动点.且满足![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,请直接写出
的锐角等腰点,请直接写出![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)直接根据锐角等腰点的概念和等腰三角形的性质逐一判断即可;
(2)先以![]() 为圆心,
为圆心,![]() 为半径画圆,然后根据数形结合,找到两个临界点,一个临界点是直线刚好与圆相切时,另一个临界点是直线刚好过点时,分别求出相应的b的值,即可确定b的范围;
为半径画圆,然后根据数形结合,找到两个临界点,一个临界点是直线刚好与圆相切时,另一个临界点是直线刚好过点时,分别求出相应的b的值,即可确定b的范围;
(3)根据题意,找到两个临界点,当点E,F在直线![]() 左侧时,过点E作
左侧时,过点E作![]() 于点M, 过点M作
于点M, 过点M作![]() 于点N,过点F作
于点N,过点F作![]() 于点G,当
于点G,当![]() 时,利用全等三角形的判定及性质求解;当点E,F在直线
时,利用全等三角形的判定及性质求解;当点E,F在直线![]() 右侧时,
右侧时,![]() ,且直线
,且直线![]() 与圆相切时,设切点为点K,过点K作
与圆相切时,设切点为点K,过点K作![]() 于点M,利用三角函数和勾股定理求解.
于点M,利用三角函数和勾股定理求解.
(1)![]() ,
,
∴![]() ,
,
∴等腰三角形的腰长为2.
∵![]() ,
,
![]() ,且
,且![]() 是锐角,满足条件,
是锐角,满足条件,
∴![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点;
的锐角等腰点;
∵![]() ,
,
![]() ,但
,但![]() 是直角,不满足条件,
是直角,不满足条件,
∴![]() 不是点
不是点![]() 关于点
关于点![]() 的锐角等腰点;
的锐角等腰点;
∵![]() ,
,
![]() ,不满足条件,
,不满足条件,
∴![]() 不是点
不是点![]() 关于点
关于点![]() 的锐角等腰点;
的锐角等腰点;
∵![]() ,
,
![]() ,不满足条件,
,不满足条件,
∴![]() 不是点
不是点![]() 关于点
关于点![]() 的锐角等腰点;
的锐角等腰点;
综上所述,是点![]() 关于点
关于点![]() 的锐角等腰点的是
的锐角等腰点的是![]() ;
;
(2) 以![]() 为圆心,
为圆心,![]() 为半径画圆,
为半径画圆,
当直线![]() 与圆相切时,设切点为点D,过点D作
与圆相切时,设切点为点D,过点D作![]() 于点E,
于点E,
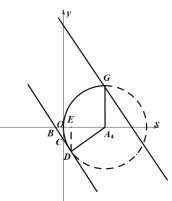
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
设![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
将点D代入![]() 中得,
中得,![]() ,
,
解得![]() ;
;
当直线![]() 过G点时,此时
过G点时,此时![]() ,
,
将点G代入![]() 中得,
中得,![]() ,
,
解得![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() ;
;
(3) 当点E,F在直线![]() 左侧时,过点E作
左侧时,过点E作![]() 于点M, 过点M作
于点M, 过点M作![]() 于点N,过点F作
于点N,过点F作![]() 于点G,
于点G,
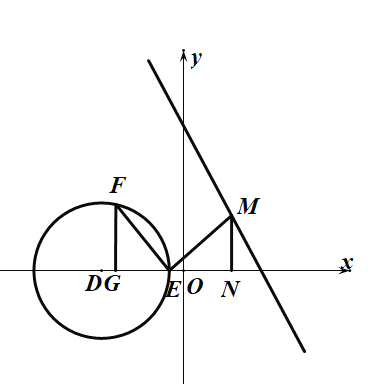
当![]() 时,
时,
∵![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
将点M代入![]() 中得,
中得,![]() ,
,
当![]() 时,直线
时,直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,
的锐角等腰点,
![]() ,
,
![]() ;
;
当点E,F在直线![]() 右侧时,
右侧时,![]() ,且直线
,且直线![]() 与圆相切时,设切点为点K,过点K作
与圆相切时,设切点为点K,过点K作![]() 于点M,
于点M,
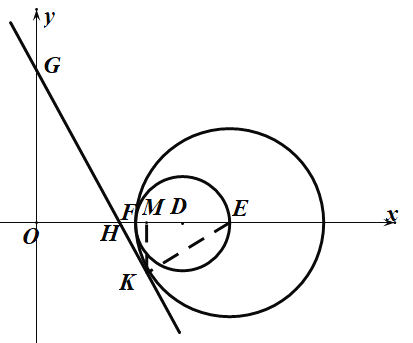
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
设![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
将点M代入![]() 中得,
中得,![]() ,
,
解得![]() ;
;
综上所述,直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,t的取值范围为
的锐角等腰点,t的取值范围为![]() .
.