题目内容
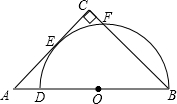
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=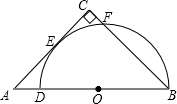 2,AD=1,则CF=________.
2,AD=1,则CF=________.
0.5
分析:首先利用三角形相似的判定方法证明△AEO∽△OMB,进而求出CE与BC的长,再利用切割线定理求出CF即可.
解答: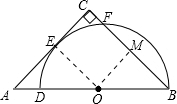 解:连接OE,做OM⊥BC,
解:连接OE,做OM⊥BC,
∵BC⊥AC,OM⊥BC,
OM∥AC,
∴∠A=∠MOB,
∴∠AEO=∠OMB,
∴△AEO∽△OMB,
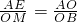 ,
,
∴OE=1,
∵AO=2,
∴AE= ,
,
解得:OM= ,
,
∴CM=OE=1,OM=CE= ,BM=
,BM= ,
,
∵CE2=CF×BC,
解得:CF=0.5.
故答案为:0.5.
点评:此题主要考查了切线的性质定理以及相似三角形的性质定理与判定定理,求出BC与CE的长是解决问题的关键.
分析:首先利用三角形相似的判定方法证明△AEO∽△OMB,进而求出CE与BC的长,再利用切割线定理求出CF即可.
解答:
 解:连接OE,做OM⊥BC,
解:连接OE,做OM⊥BC,∵BC⊥AC,OM⊥BC,
OM∥AC,
∴∠A=∠MOB,
∴∠AEO=∠OMB,
∴△AEO∽△OMB,
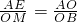 ,
,∴OE=1,
∵AO=2,
∴AE=
 ,
,解得:OM=
 ,
,∴CM=OE=1,OM=CE=
 ,BM=
,BM= ,
,∵CE2=CF×BC,
解得:CF=0.5.
故答案为:0.5.
点评:此题主要考查了切线的性质定理以及相似三角形的性质定理与判定定理,求出BC与CE的长是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 2,AD=1,则CF=
2,AD=1,则CF= 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 于点F.
于点F.