题目内容
1. 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点B的坐标为(1,1),点E的坐标为($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点B的坐标为(1,1),点E的坐标为($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).
分析 在正方形中四边都相等,由反比例的性质可知S□OABC=1,即OA=1.若假设点E的纵坐标为m,则横坐标为1+m,因为在反比例函数图象上任意一点的横坐标和纵坐标之积都等于比例系数k=1,所以可列方程进行解答.
解答 解:依据比例系数k的几何意义可得正方形OABC的面积为1,
所以其边长为1,故B(1,1).
设点E的纵坐标为m,则横坐标为1+m,
所以m(1+m)=1,
解得m1=$\frac{-1+\sqrt{5}}{2}$,m2=$\frac{-1-\sqrt{5}}{2}$,
由于m=$\frac{-1-\sqrt{5}}{2}$不合题意,所以应舍去,
故m=$\frac{-1+\sqrt{5}}{2}$,
即1+m=$\frac{1+\sqrt{5}}{2}$,
故点E的坐标是($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).
故答案是:(1,1);($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).
点评 本题主要考查的是反比例函数的图象和性质,掌握反比例函数图象上任意一点的横纵坐标的乘积等于定值k是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
9.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3÷(a3)3=1 | C. | (a2b)3÷(-ab)2=-a4b | D. | (a3)2•a5=a11 |
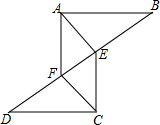 如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边. 作图题:
作图题: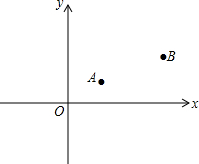 如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.
如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).