题目内容
 在梯形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为
在梯形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为
- A.矩形
- B.菱形
- C.梯形
- D.平行四边形
B
分析:首先由折叠的性质可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,又由AD∥BC,即可证得△CDE是等腰三角形,可得CD=CE,然后根据四条边都相等的四边形是菱形,即可证得四边形CDC′E为菱形.
解答:四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠CED,
∴∠CDE=∠CED,
∴CD=CE,
∴CD=C′D=C′E=CE,
∴四边形CDC′E为菱形.
故选B.
点评:此题考查了折叠的性质,等腰三角形的判定与性质以及菱形的判定等知识.此题难度适中,解题的关键是注意数形结合思想的应用,注意根据折叠的性质找到对应边与对应角.
分析:首先由折叠的性质可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,又由AD∥BC,即可证得△CDE是等腰三角形,可得CD=CE,然后根据四条边都相等的四边形是菱形,即可证得四边形CDC′E为菱形.
解答:四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠CED,
∴∠CDE=∠CED,
∴CD=CE,
∴CD=C′D=C′E=CE,
∴四边形CDC′E为菱形.
故选B.
点评:此题考查了折叠的性质,等腰三角形的判定与性质以及菱形的判定等知识.此题难度适中,解题的关键是注意数形结合思想的应用,注意根据折叠的性质找到对应边与对应角.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 19、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连接C′E.
19、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连接C′E. 23、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连接C′E.
23、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连接C′E.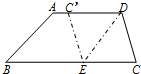 21、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C’处,折痕DE交BC于点E,连接C’E,试判断四边形CDC’E是什么特殊四边形,并说明理由.
21、如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C’处,折痕DE交BC于点E,连接C’E,试判断四边形CDC’E是什么特殊四边形,并说明理由.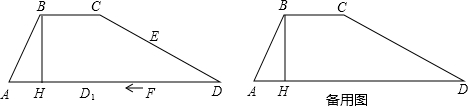
 在梯形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为( )
在梯形纸片ABCD中,AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为( )