题目内容
在正方形ABCD中,点E是对角线BD上一点,且BD=
AE,则∠BAE= .
| 3 |
考点:正方形的性质
专题:分类讨论
分析:如图,利用正方形的性质,不妨设BD=a,表示出AO,进一步由BD=
AE,表示出AE,在直角三角形AOE中,利用锐角三角函数cos∠EAO求得数值,进一步求得角度即可;分两种情况探讨答案:E在OB或OD上.


| 3 |


解答:解:如图:

∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,OA=OB=OC=OD
设BD=a,则OA=
AC=
BD=
a
∵BD=
AE,
∴AE=
a
在直角△AOE中,
cos∠EAO=
=
=
∴∠EAO=30°
∴∠BAE=∠BAO-∠EAO=45°-30°=15°.
同理如图:

求得∠BAE=∠BAO+∠EAO=45°+30°=75°.
综上所知∠BAE=15°或75°.
故答案为:15°或75°.

∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,OA=OB=OC=OD
设BD=a,则OA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BD=
| 3 |
∴AE=
| ||
| 3 |
在直角△AOE中,
cos∠EAO=
| AO |
| AE |
| ||||
|
| ||
| 2 |
∴∠EAO=30°
∴∠BAE=∠BAO-∠EAO=45°-30°=15°.
同理如图:

求得∠BAE=∠BAO+∠EAO=45°+30°=75°.
综上所知∠BAE=15°或75°.
故答案为:15°或75°.
点评:此题考查正方形的性质,特殊角的三角函数,注意取一个参数值,进一步利用正方形性质解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,真命题是( )
| A、对角线相等的四边形是平行四边形 |
| B、对角线互相垂直且平分的四边形是正方形 |
| C、对角线互相垂直的四边形是菱形 |
| D、四个角相等的四边形是矩形 |
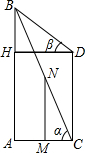 如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)
如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)