题目内容
10. 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).(1)当t=1时,求点D的坐标;
(2)设△POD的面积为S,求S关于t的函数关系式;
(3)在P的运动过程中,是否存在某一时刻,使得△PBE为等腰三角形?若存在,请求出满足条件的t的值;若不存在,请说明理由.
分析 (1)如图1中,先证明△APB≌△DQP,得AP=DQ,由此即可解决问题.
(2)首先证明△APB≌△DQP,得AP=DQ,再根据S△POD=$\frac{1}{2}$×OP×DQ即可解决问题.
(3)如图2中,连接BO交PE于G.先证明△PBD是等腰直角三角形,再分两种情形①BP=BE,②EB=EP求解即可.
解答 解:(1)如图1中,
t=1时,AP=OQ=1,
∴AO=PQ,
∵四边形AOCB是正方形,
∴AB=AO=PQ,
∵∠BPD=∠DQP=90°,
∴∠APB+∠DPQ=90°,∠DPQ+∠PDQ=90°,
∴∠APB=∠PDQ,
在△PAB和△DQP中,
$\left\{\begin{array}{l}{∠APB=∠PDQ}\\{∠PAB=∠DQP=90°}\\{AB=PQ}\end{array}\right.$,
∴△PAB≌△DQP,
∴PA=DQ=1,
∴点D坐标(1,1).
(2)AP=OQ=t,
∴AO=PQ,
∵四边形AOCB是正方形,
∴AB=AO=PQ,
∵∠BPD=∠DQP=90°,
∴∠APB+∠DPQ=90°,∠DPQ+∠PDQ=90°,
∴∠APB=∠PDQ,
在△PAB和△DQP中,
$\left\{\begin{array}{l}{∠APB=∠PDQ}\\{∠PAB=∠DQP=90°}\\{AB=PQ}\end{array}\right.$,
∴△PAB≌△DQP,
∴PA=DQ=t,
∴S△POD=$\frac{1}{2}$×OP×DQ=$\frac{1}{2}$×(4-t)•t=-$\frac{1}{2}$t2+2t.(0<t≤4).
(3)如图2中,连接BO交PE于G.
∵△PAB≌△DQP,
∴PB=PD,∵∠BPD=90°,
∴∠PBD=∠PDB=45°,
∵△PBE是等腰三角形,
∴有两种可能①BP=BE,②BE=PE,
①当BP=BE时,在Rt△BAP和Rt△BCE中,
$\left\{\begin{array}{l}{BP=BE}\\{BA=BC}\end{array}\right.$,
∴△BAP≌△BCE,
∴AP=EC,∵OA=OC,∠ABP=∠CBE=22.5°,
∴OP=OE.
∴OB垂直平分线段PE,
∴∠PBO=∠EBO=22.5°,
∴∠PBA=∠PBO,
∵PA⊥AB,PG⊥BO,
∴PA=PG,
∵∠AOB=45°,
∴∠GPO=∠GOP=45°,
∴PA=PG=GO,
设PA=PG=GO=x,则OP=$\sqrt{2}$x,
∴x+$\sqrt{2}$x=4,
∴x=4$\sqrt{2}$-4,
∴t=4$\sqrt{2}$-4,
②EB=PE时,点P与点O重合,此时t=4,
综上所述t=4$\sqrt{2}$-4或4秒时,△PBE是等腰三角形.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、三角形的面积公式等知识,解题的关键是正确寻找全等三角形,学会分类讨论,属于中考常考题型.

| A. | (-2)2<(-2)3 | B. | -32<(-2)3 | C. | -$\frac{9}{10}$>-$\frac{8}{9}$ | D. | -0.3<-$\frac{1}{3}$ |
| A. | m=-1 | B. | m=3 | C. | m≤3 | D. | m≥-3 |
 如图1,在一张长40cm,宽25cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图2的无盖纸盒,若纸盒的底面积是450cm2,则纸盒的高是多少?
如图1,在一张长40cm,宽25cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图2的无盖纸盒,若纸盒的底面积是450cm2,则纸盒的高是多少?
 ,-2,-
,-2,- 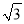 的大小,其中最小的实数是( ).
的大小,其中最小的实数是( ). C. -2 D. -
C. -2 D. -