Question

【题目】已知菱形OABC的边长为5，且tan∠AOC＝，点E是线段BC的中点，过点A、E的抛物线y＝ax2+bx+c与边AB交于点D．

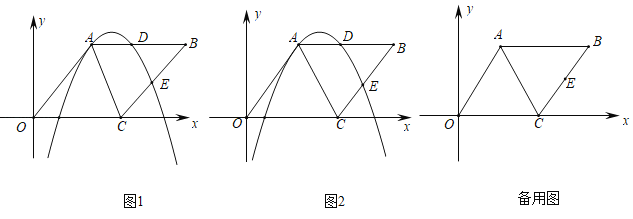
（1）求点A和点E的坐标；

（2）连结DE，将△BDE沿着DE翻折．

①当点B的对应点B'恰好落在线段AC上时，求点D的坐标；

②连接OB、BB'，请直接写出此时该抛物线二次项系数a＝　 　．

Answer 1

【答案】（1）A（3，4），E（，2）；

（2）①D（）或D（）．②．

【解析】

（1）过点A作x轴的垂线，垂足为F,由条件可得OF＝3，AF＝4，则A点坐标可求出，求出B，C的坐标，则E点坐标可求出；

（2）①求出直线AC的解析式为y＝﹣2x+10，设D（m，4），由BD＝B'D可得m的方程，则D点坐标可求出；

②抛物线y＝ax2+bx+c过点A，E，D三点，由待定系数法可求出a的值．

解：（1）如图，过点A作x轴的垂线，垂足为F，

∵OA＝5，且tan∠AOC＝，

∴OF＝3，AF＝4，即A（3，4），

又∵四边形OABC为菱形，

∴OA＝OC＝BC＝AB＝5，

∴B（8，4），C（5，0），

∴E（，2），

（2）①设AC：y＝kx+m，把A（3，4）和C（5，0）代入得

k＝﹣2，m＝10，

∴y＝﹣2x+10，

设B'（x，﹣2x+10），由BE＝B'E可得（6.5﹣x）2+（2x﹣8）2＝2.52，

解得x＝4或x＝5，

∴B'（4，2）或（5，0），

设D（m，4），由BD＝B'D可得（m﹣4）2+4＝（8﹣m）2或（m﹣5）2+16＝（8﹣m）2，

解得m1=，m2＝

∴D（）或D（）．

②若抛物线y＝ax2+bx+c过点A（3，4），E（，2），D（，4），

∴解得a=-，

若抛物线y＝ax2+bx+c过点A（3，4），E（，2），D（4），

∴，解得a＝．

故答案为：．