题目内容
已知二次函数y=x2-(m-1)x+m2-2m-3,其中m为实数,图象经过原点.
(1)求二次函数的表达式;
(2)怎样平移此函数图象,使它在x>2时,y随x的增大而增大,在x<2时,y随x的增大而减小?
(1)求二次函数的表达式;
(2)怎样平移此函数图象,使它在x>2时,y随x的增大而增大,在x<2时,y随x的增大而减小?
考点:待定系数法求二次函数解析式,二次函数图象与几何变换
专题:
分析:(1)根据二次函数图象上点的坐标特征,把原点坐标代入解析式得到m2-2m-3=0,解m的一元二次方程得到m1=3,m2=-1,于是可确定二次函数解析式;
(2)先根据二次函数的性质确定平移后二次函数图象的对称轴为直线x=2,再把(1)中的解析式配成顶点式y=(x-1)2-1或y=(x+1)2-1,然后根据二次函数图象与几何变换的规律求解.
(2)先根据二次函数的性质确定平移后二次函数图象的对称轴为直线x=2,再把(1)中的解析式配成顶点式y=(x-1)2-1或y=(x+1)2-1,然后根据二次函数图象与几何变换的规律求解.
解答:解:(1)把(0,0)代入得m2-2m-3=0,解得m1=3,m2=-1,
所以二次函数解析式为y=x2-2x或y=x2+2x;
(2)因为平移后的二次函数当x>2时,y随x的增大而增大,在x<2时,y随x的增大而减小,
所以平移后的二次函数图象的对称轴为直线x=2,
对于二次函数y=x2-2x=(x-1)2-1,抛物线的对称轴为直线x=1,所以把y=x2-2x向右平移1个单位;
对于二次函数y=x2+2x=(x+1)2-1,抛物线的对称轴为直线x=-1,所以把y=x2-2x向右平移3个单位.
所以二次函数解析式为y=x2-2x或y=x2+2x;
(2)因为平移后的二次函数当x>2时,y随x的增大而增大,在x<2时,y随x的增大而减小,
所以平移后的二次函数图象的对称轴为直线x=2,
对于二次函数y=x2-2x=(x-1)2-1,抛物线的对称轴为直线x=1,所以把y=x2-2x向右平移1个单位;
对于二次函数y=x2+2x=(x+1)2-1,抛物线的对称轴为直线x=-1,所以把y=x2-2x向右平移3个单位.
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了轴对称-最短路线问题.

练习册系列答案
相关题目
组织学生去科技馆参观,估计共需其费用120元,后来又有2个参加进来,总费用不变,于是每人可少分摊3元,原来这组学生人数是( )
| A、8人 | B、10人 |
| C、12人 | D、15人 |
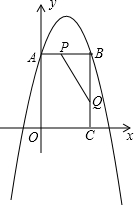 如图所示,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的正半轴和x轴的正半轴上,抛物线y=ax2+bx+c(a≠0)经过点A、B,且18a+c=0.
如图所示,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的正半轴和x轴的正半轴上,抛物线y=ax2+bx+c(a≠0)经过点A、B,且18a+c=0. 现有4张卡片写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
现有4张卡片写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题: 如图,在四边形ABCD中,点E在AB上,CE∥AD,且BE=CE,∠B-∠A=30°,求∠A、∠B的度数.
如图,在四边形ABCD中,点E在AB上,CE∥AD,且BE=CE,∠B-∠A=30°,求∠A、∠B的度数. 如图所示,AO⊥OB,AC∥OB,AO=1,求阴影部分的面积.
如图所示,AO⊥OB,AC∥OB,AO=1,求阴影部分的面积.