题目内容
函数y=ax+b，当x=1时，y=1；当x=-1时，y=-5．求函数解析式．
考点：待定系数法求一次函数解析式
专题：
分析：把所给条件代入函数解析式得到关于a、b的二元一次方程组，解得a、b即可得出函数解析式．
解答：解：
∵当x=1时，y=1；当x=-1时，y=-5，
∴代入解析式可得
，
解得
，
∴函数解析式为：y=3x-2．
∵当x=1时，y=1；当x=-1时，y=-5，
∴代入解析式可得
|
解得
|
∴函数解析式为：y=3x-2．
点评：本题主要考查待定系数法求函数解析式，把条件代入得到关于a、b的方程组是解题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
若方程（a-2）x|a|-3x=1是关于x的一元二次方程，则a是（ ）
| A、2 | B、-2 | C、±2 | D、±1 |
已知：右图是二次函数y=（x-m）2+k的图象，其顶点坐标为M（1，-4）．
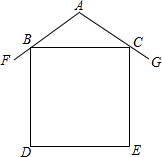我市新农村建设推动了农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡AF、AG分别架在墙体的点B、点C处，且AB=AC，侧面四边形BDEC为矩形，若测得∠FAG=100°，则∠FBD=（ ）| A、35° | B、40° |
| C、50° | D、70° |
若x1，x2（x1＜x2）是关于x的方程（x-a）（x-b）=a-b（a＜b）的两个根，则实数x1，x2，a，b的大小关系为（ ）
| A、x1＜x2＜a＜b |
| B、x1＜a＜b＜x2 |
| C、a＜x1＜x2＜b |
| D、a＜x1＜b＜x2 |
已知长方形ABCD，AD=6cm，AB=5cm，L、M是CD的中点，N、O、P、Q是AD、BC的三等分点，则阴影部分的面积是