Question

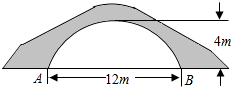如图为一座拱桥的示意图，当水面宽AB为12m时，桥洞顶部离水面4m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点B为坐标原点时的抛物线解析式是y=-

1

9

（x+6）²+4，则选取点A为坐标原点时的抛物线解析式是

 

．

Answer 1

考点：二次函数的应用

专题：

分析：直接利用抛物线顶点坐标的位置变化得出相当于抛物线y=-

1

9

（x+6）²+4向左平移12个单位，进而得出答案．

解答：解：由题意可得：相当于抛物线y=-

1

9

（x+6）²+4向左平移12个单位，
故选取点A为坐标原点时的抛物线解析式是：y=-

1

9

（x+18）²+4．
故答案为：y=-

1

9

（x+18）²+4．

点评：此题主要考查了二次函数的应用，根据题意得出顶点坐标的变化规律是解题关键．