题目内容
8．若$\frac{a}{5}$=$\frac{b}{7}$=$\frac{c}{8}$，且3a-2b+c=3，求2a+4b-3c的值．分析 根据等式的性质，可得x表示a，b，c，根据解方程，可得答案．
解答 解：设$\frac{a}{5}$=$\frac{b}{7}$=$\frac{c}{8}$=x，
a=5x，b=7x，c=8x．
3a-2b+c=3，
15x-14x+8x=3．
解得x=$\frac{1}{3}$，
a=5x=$\frac{5}{3}$，b=7x=$\frac{7}{3}$，c=8x=$\frac{8}{3}$．
2a+4b-3c=2×$\frac{5}{3}$+4×$\frac{7}{3}$-3×$\frac{8}{3}$=$\frac{14}{3}$．
点评 本题考查了比例的性质，利用等式的性质得出x表示a，b，c是解题关键．
练习册系列答案
相关题目
1．
如图，下列各点在阴影区域内的是（ ）
如图，下列各点在阴影区域内的是（ ）| A． | （-$\frac{1}{2}$，4） | B． | （3，-2） | C． | （-5，5） | D． | （-2，-1） |
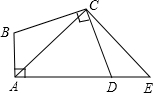如图，在四边形ABCD中，∠BAD=∠BCD=90°，BC=CD，E是AD延长线上一点，若DE=AB=3cm，CE=4$\sqrt{2}$cm，连接AC，BD．