题目内容
如图，D为△ABC内一点，E为△ABC外一点，且∠1=∠2，∠3=∠4，找出图中的两对相似三角形并说明理由．
解：△ABD∽△CBE，△ABC∽△DBE．
∵∠1=∠2，∠3=∠4，
∴△ABD∽△CBE，
∴
∵∠1=∠2，
∴∠ABC=∠DBE，
∴△ABC∽△DBE
分析：根据相似三角形的判定定理：两角相等；对应边成比例且夹角相等即可证明．
点评：此题主要考查相似三角形的判定定理的理解和掌握，比较简单，属于基础题．
∵∠1=∠2，∠3=∠4，
∴△ABD∽△CBE，
∴
∵∠1=∠2，
∴∠ABC=∠DBE，
∴△ABC∽△DBE
分析：根据相似三角形的判定定理：两角相等；对应边成比例且夹角相等即可证明．
点评：此题主要考查相似三角形的判定定理的理解和掌握，比较简单，属于基础题．
练习册系列答案
相关题目
23、已知：如图，D为△ABC内一点，AC=BC，CD平分∠ACB．
如图，D为△ABC内一点，E为△ABC外一点，且∠1=∠2，∠3=∠4．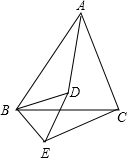
已知，如图，D为△ABC内一点连接BD、AD，以BC为边在△ABC外作∠CBE=∠ABD，∠BCE=∠BAD，BE、
如图，O为△ABC内一点，以O为位似中心，作△A′B′C′∽△ABC，且相似比为2．