题目内容
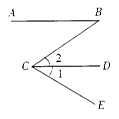
如图，AB∥CD，证明：∠A=∠C+∠P．
证明：∵AB∥CD，
∴∠A=∠PED，（两直线平行，同位角相等）
又∠PED为△PCE的外角，
∴∠P+∠C=∠PED，
∴∠P+∠C=∠A．
分析：因为∠PED为△PCE的外角，所以∠P+∠C=∠PED；再根据两直线平行，同位角相等可得∠A=∠PED，即∠A=∠C+∠P．
点评：本题考查三角形外角的性质及平行线的性质，解答的关键是沟通外角和内角的关系．
∴∠A=∠PED，（两直线平行，同位角相等）
又∠PED为△PCE的外角，
∴∠P+∠C=∠PED，
∴∠P+∠C=∠A．
分析：因为∠PED为△PCE的外角，所以∠P+∠C=∠PED；再根据两直线平行，同位角相等可得∠A=∠PED，即∠A=∠C+∠P．
点评：本题考查三角形外角的性质及平行线的性质，解答的关键是沟通外角和内角的关系．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
2、如图，AB=CD，AC=BD，且AC交BD于点O，在原图形的基础上，要利用“SSS”证△AOB≌△DOC，可以添加的条件是（ ）
如图，AB=CD，要证△ABC≌△CDA，则还需添加一个条件是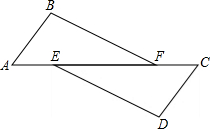
如图，AB=CD，BF=DE，E、F是AC上两点，且AE=CF，欲证∠B=∠D，可先运用等式的性质证明AF=
