题目内容
 如图,是某高速公路圆弧形隧道,其中路面宽10米,净高7米,则此隧道半径是( )
如图,是某高速公路圆弧形隧道,其中路面宽10米,净高7米,则此隧道半径是( )| A、5米 | ||
B、
| ||
C、
| ||
| D、7米 |
分析:连接OA,由垂径定理易得出AC的长度,在Rt△OAC中,可用半径表示出OC的长,根据勾股定理即可求出半径的长度.
解答: 解:连接OA;
解:连接OA;
Rt△OAC中,AC=
AB=5米;
设⊙O的半径为R,则OA=OD=R,OC=7-R;
由勾股定理,得:OA2=AC2+OC2,即:
R2=(7-R)2+52,解得R=
(米);
故选B.
 解:连接OA;
解:连接OA;Rt△OAC中,AC=
| 1 |
| 2 |
设⊙O的半径为R,则OA=OD=R,OC=7-R;
由勾股定理,得:OA2=AC2+OC2,即:
R2=(7-R)2+52,解得R=
| 37 |
| 7 |
故选B.
点评:此题主要考查的是垂径定理及勾股定理的应用.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
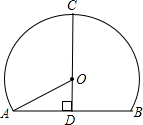 如图,是一个某一高速公路单心圆曲隧道的截面,若路面AB宽为12米,净高CD为8米,则此隧道单心圆的半径OA是
如图,是一个某一高速公路单心圆曲隧道的截面,若路面AB宽为12米,净高CD为8米,则此隧道单心圆的半径OA是 如图,是某高速公路圆弧形隧道,其中路面宽10米,净高7米,则此隧道半径是
如图,是某高速公路圆弧形隧道,其中路面宽10米,净高7米,则此隧道半径是 米
米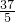 米
米

 米
米 米
米