题目内容
18. 如图,AB是半圆的直径,点D是$\widehat{AC}$的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,点D是$\widehat{AC}$的中点,∠ABC=50°,则∠DAB等于( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
分析 连结BD,由于点D是$\widehat{AC}$的中点,即$\widehat{CD}$=$\widehat{AD}$,根据圆周角定理得∠ABD=∠CBD,则∠ABD=25°,再根据直径所对的圆周角为直角得到∠ADB=90°,然后利用三角形内角和定理可计算出∠DAB的度数.
解答 解:连结BD,如图,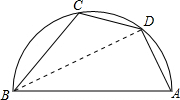
∵点D是$\widehat{AC}$的中点,即$\widehat{CD}$=$\widehat{AD}$,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=$\frac{1}{2}$×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠DAB=90°-25°=65°.
故选A.
点评 本题考查了圆周角定理及其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直径所对的圆周角为直角.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (-2a2)3÷($\frac{a}{2}$)2=-16a4 | ||
| C. | 3a-1=$\frac{1}{3a}$ | D. | (2$\sqrt{3}$a2-$\sqrt{3}$a)2÷3a2=4a2-4a+1 |
9.在函数y=$\sqrt{1-5x}$中,自变量x的取值范围是( )
| A. | x<$\frac{1}{5}$ | B. | x≤$\frac{1}{5}$ | C. | x$>\frac{1}{5}$ | D. | x≥$\frac{1}{5}$ |
13.下列图形中,轴对称图形的个数( )


| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
3. 如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
 如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )
如图是太原市某日八个整点的空气质量趋势图(空气指数越大越严重),根据图中的空气指数可知这组数据的中位数是( )| A. | 64 | B. | 60 | C. | 56 | D. | 48 |
7.十边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
 如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为34°.
如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为34°.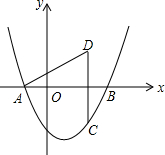 如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),
如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),