题目内容
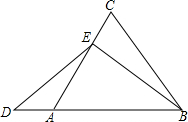 已知在△ABC中,AC=BC,点E为AC上一点,点D为BC延长线上一点,DA=kCE.当∠C=60°,k=1时,求证:DE=BE.
已知在△ABC中,AC=BC,点E为AC上一点,点D为BC延长线上一点,DA=kCE.当∠C=60°,k=1时,求证:DE=BE.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:过D作DF∥BC交AC的延长线于F点,根据等边三角形的性质得到∠CAB=∠ACB=60°,则∠F=60°,∠DAF=60°,得到△DAF为等边三角形,于是DA=AF=DF,易得EF=BC,根据三角形全等的判定可得到△EDF≌△BEC,即可得到结论.
解答:证明:∵∠C=60°,AC=BC,
∴△ABC是等边三角形,
过D作DF∥BC交CA的延长线于F点,如图,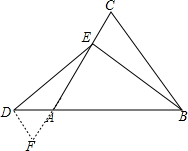
∵△ABC为等边三角形,
∴∠CAB=∠C=60°,AB=AC,
∴∠F=∠C=60°,∠DAF=∠CAB=60°,
∴△ACF为等边三角形,
∴DA=AF=DF,
而AD=CE,
∴DF=CE=AF,BC=AC=EF,
在△BCE和△EFD中,
∴△BCE≌△EFD(SAS),
∴DE=BE.
∴△ABC是等边三角形,
过D作DF∥BC交CA的延长线于F点,如图,

∵△ABC为等边三角形,
∴∠CAB=∠C=60°,AB=AC,
∴∠F=∠C=60°,∠DAF=∠CAB=60°,
∴△ACF为等边三角形,
∴DA=AF=DF,
而AD=CE,
∴DF=CE=AF,BC=AC=EF,
在△BCE和△EFD中,
|
∴△BCE≌△EFD(SAS),
∴DE=BE.
点评:本题考查了等边三角形的判定与性质和全等三角形的性质和判定的应用,注意:有一个内角为60°的等腰三角形为等边三角形;等边三角形的三个内角都等于60°,三边都相等.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD∥AC.求证:
如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD∥AC.求证:

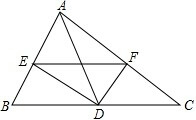 如图,在△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE、DF分别交AB、AC于E、F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
如图,在△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE、DF分别交AB、AC于E、F,且BE2+CF2=EF2,求证:△ABC为直角三角形. 已知二次函数y=2x2
已知二次函数y=2x2