题目内容
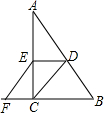 已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.
已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;
(2)若EF=2cm,求AB的长.
考点:平行四边形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)由三角形中位线定理推知ED∥FC;然后结合已知条件“EF∥DC”,利用“有两组对边相互平行的四边形为平行四边形”证得结论;
(2)根据“在直角三角形中,斜边上的中线等于斜边的一半”得到AB=2DC.
(2)根据“在直角三角形中,斜边上的中线等于斜边的一半”得到AB=2DC.
解答:(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC=
AB,
∴AB=2DC=4cm.
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC=
| 1 |
| 2 |
∴AB=2DC=4cm.
点评:本题考查了平行四边形的判定与性质以及直角三角形斜边上的中线.此题中,在利用“在直角三角形中,斜边上的中线等于斜边的一半”时,要点明点D是Rt△ABC斜边AB的中点后,方可得到DC=
AB.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
-2的相反数是( )
A、1+
| ||
B、1-
| ||
| C、2 | ||
| D、-2 |
矩形具有而平行四边形不一定具有的性质是( )
| A、两组对边平行且相等 |
| B、四个内角的和等于360° |
| C、不稳定性 |
| D、四个内角和都是直角 |
平面直角坐标系中,点P(m,m-2)在第四象限,则m的取值范围是( )
| A、m>2 | B、m<0 |
| C、0<m<2 | D、0≤m≤2 |
为了求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,所以1+2+22+23+…+22014=22015-1.仿照以上推理计算出1+5+52+53+…+52014的值是( )
| A、52015-1 | ||
| B、52016-1 | ||
C、
| ||
D、
|
 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.DF⊥AC于点F.