题目内容
 如图,BC切圆O于B,AB=BC=OA,连AC交圆O于D,OC交圆O于E,则∠CED的度数为
如图,BC切圆O于B,AB=BC=OA,连AC交圆O于D,OC交圆O于E,则∠CED的度数为考点:切线的性质,圆内接四边形的性质
专题:
分析:由∠CED在圆的外部,所以尽可能让它成为圆内接四边形的外角,需在圆中构造四边形,利用已知条件,得出所有能得出的角度,只要求出圆内接四边形与∠CED有关的内角,即可求出∠CED的度数.
解答:解:延长CO到圆上一点M,连接MA,
∵BC切圆O于B,
∴∠OBC=90°,
又∵AB=BC=OA=BO,
∴△OAB是等边三角形,∠BAC=∠BCA,
BO=BC,∴∠BOC=∠BCO=45°
又∵∠OBA=60°,
∴∠BAC=∠BCA=15°,
∵∠AOB=60°,∠BOC=45°,
∴∠OMA=75°,
∵OM=0A,
∴∠MAO=52.5°,
∴∠MAC=97.5°,
∠CED=∠MAC=97.5°(圆内接四边形的外角等于它不相邻的内角).
∵BC切圆O于B,
∴∠OBC=90°,
又∵AB=BC=OA=BO,

∴△OAB是等边三角形,∠BAC=∠BCA,
BO=BC,∴∠BOC=∠BCO=45°
又∵∠OBA=60°,
∴∠BAC=∠BCA=15°,
∵∠AOB=60°,∠BOC=45°,
∴∠OMA=75°,
∵OM=0A,
∴∠MAO=52.5°,
∴∠MAC=97.5°,
∠CED=∠MAC=97.5°(圆内接四边形的外角等于它不相邻的内角).
点评:主要考查了切线的性质,等腰三角形的性质,圆内接四边形的性质,综合性较强,有利于同学们综合能力的提升.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在同一时刻的阳光下,甲的影子比乙的影子长,那么在同一路灯下( )
| A、甲的影子比乙的长 |
| B、甲的影子比乙的影子短 |
| C、甲的影子和乙的影子一样长 |
| D、无法判断 |
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
则下列说法错误的是( )
| x | … | -1 | 0 | 1 | 2 | 3 | … | ||||||||||
| y | … |
|
|
|
|
|
… |
| A、二次函数图象与x轴交点有两个 |
| B、x≥2时y随x的增大而增大 |
| C、二次函数图象与x轴交点横坐标一个在-1~0之间,另一个在2~3之间 |
| D、对称轴为直线x=1.5 |
 如图,已知点A是一次函数y=2x的图象与反比例函数y=
如图,已知点A是一次函数y=2x的图象与反比例函数y=| k |
| x |
| A、(-8,0) | ||
| B、(-6,0) | ||
C、(-
| ||
D、(-
|
 如图,A1A2⊥A2A3,A2A3⊥A3A4,…,设AA1=A1A2=A2A3=1,若A1A2=a1,A3A4=a2,A5A6=a3,则a2=
如图,A1A2⊥A2A3,A2A3⊥A3A4,…,设AA1=A1A2=A2A3=1,若A1A2=a1,A3A4=a2,A5A6=a3,则a2= 在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长是
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长是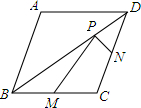 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.
已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.