题目内容
在△ABC中，AD是高，矩形PQMN的顶点P、N分别在AB、AC上，QM在边BC上．若BC=8cm，AD=6cm，且PN=2PQ，则矩形PQMN的周长是考点：相似三角形的判定与性质,矩形的性质
专题：
分析：由题意可得出PQ：AD=BP：AB，PN：BC=AP：AB，BC=8，AD=6，据此可得出PQ，PN的值，故可得出矩形PQMN的周长．
解答：解：由题意得；PQ：AD=BP：AB，PN：BC=AP：AB
∴
+
=
+
=
=
=1，
又∵PN=2PQ，BC=8cm，AD=6cm，
∴
+
=1，
∴PQ=2.4
则PN=4.8，
∴矩形PQMN的周长=14.4cm．
∴
| PQ |
| AD |
| PN |
| BC |
| BP |
| AB |
| AP |
| AB |
| AP+PB |
| AB |
| AB |
| AB |
又∵PN=2PQ，BC=8cm，AD=6cm，
∴
| PQ |
| 6 |
| 2PQ |
| 8 |
∴PQ=2.4
则PN=4.8，
∴矩形PQMN的周长=14.4cm．
点评：本题考查了相似三角形的性质，能够灵活运用比例线段解决本题的关键，技巧性很强，要注意掌握做题技巧性．
练习册系列答案
相关题目
如图，△ABC是等腰直角三角形，点D是斜边BC中点，△ABD绕点A旋转到△ACE的位置，恰与△ACD组成正方形ADCE，则△ABD所经过的旋转是（ ）| A、顺时针旋转225° |
| B、逆时针旋转45° |
| C、顺时针旋转315° |
| D、逆时针旋转90° |
计算(-2)2005•(
)2005等于（ ）
| 1 |
| 2 |
| A、-2 | ||
B、
| ||
| C、1 | ||
| D、-1 |
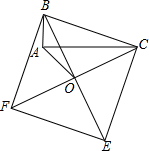如图，以Rt△ABC的斜边BC为一边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连结AO，如果AB=4，AO=7
如图：割线ABC过圆心O点，且D是
如图，BC切圆O于B，AB=BC=OA，连AC交圆O于D，OC交圆O于E，则∠CED的度数为若|a|=1，b=3，则a+b的值为（ ）
| A、4或2 | B、2 | C、4 | D、-2 |