题目内容
如图，已知AB=5cm，BC=2cm，点O是线段AC的中点O，求线段OB的长．
解：∵AB=5，BC=2，
∴AC=AB+BC=5+2=7；
又∵点O是线段AC的中点，
∴AO=
AC=×7=3.5，
∴OB=AB-AO=5-3.5=1.5．
分析：由B在线段AC上可知AC=AB+BC，把AB=5，BC=2代入即可得线段AC的长；再根据O是线段AC的中点及AC的长可求出OA的长，由OB=AB-AO即可得出答案．
点评：本题考查的是两点间的距离，利用数形结合求解是解答此类题目的关键．
∴AC=AB+BC=5+2=7；
又∵点O是线段AC的中点，
∴AO=
AC=×7=3.5，∴OB=AB-AO=5-3.5=1.5．
分析：由B在线段AC上可知AC=AB+BC，把AB=5，BC=2代入即可得线段AC的长；再根据O是线段AC的中点及AC的长可求出OA的长，由OB=AB-AO即可得出答案．
点评：本题考查的是两点间的距离，利用数形结合求解是解答此类题目的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
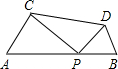如图，已知AB=10，P是线段AB上任意一点，在AB的同侧分别以AP和PB为边作两个等边三角形APC和BPD，则线段CD的长度的最小值是（ ）| A、4 | ||
| B、5 | ||
| C、6 | ||
D、5(
|
如图，已知AB∥CD∥EF，BD：DF=2：5，那么下列结论正确的是（ ）| A、AC：AE=2：5 | B、AB：CD=2：5 | C、CD：EF=2：5 | D、CE：EA=5：7 |
如图，已知AB为⊙O的弦，OC⊥AB，垂足为C，若OA=5，AB=8，则弦心距OC的长为（ ）| A、6 | B、5 | C、3 | D、4 |
如图，已知AB⊥CD，△ABD，△BCE都是等腰直角三角形，如果CD=8，BE=3，则AC等于（ ）
如图，已知AB=6，AC=9，DC=6，要使△ABD≌△DCA，还需增加的条件是（ ）