题目内容
11. 如图,△ABC的面积为600,且BC=30,某工人从这个三角形中切割出三个相同的正方形,如图所示,求正方形零件的边长.
如图,△ABC的面积为600,且BC=30,某工人从这个三角形中切割出三个相同的正方形,如图所示,求正方形零件的边长.
分析 作AM⊥BC于M,交EF于N,如图,先利用三角形面积公式计算出AM=40,设正方形零件的边长为x,则EF=x,MN=2x,AN=AM-MN=40-2x,再证明△AEF∽△ABC,利用相似比可得$\frac{40-2x}{40}$=$\frac{x}{30}$,然后利用比例性质求出x即可.
解答 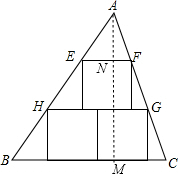 解:作AM⊥BC于M,交EF于N,如图,
解:作AM⊥BC于M,交EF于N,如图,
∵△ABC的面积为600,
∴$\frac{1}{2}$•30•AM=600,
∴AM=40,
设正方形零件的边长为x,则EF=x,MN=2x,AN=AM-MN=40-2x,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AN}{AM}$=$\frac{EF}{BC}$,即$\frac{40-2x}{40}$=$\frac{x}{30}$,解得x=12,
即正方形零件的边长为12.
点评 本题考查了相似三角形的应用:通过构造“A”型或“X”型相似图,用相似三角形对应边的比相等的性质求线段的长.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,AB,CD是⊙O的直径,AE,CF是弦,且AE=CF.求证:∠A=∠C.
如图,AB,CD是⊙O的直径,AE,CF是弦,且AE=CF.求证:∠A=∠C.