题目内容
19.数轴上离开原点距离为$\sqrt{2}$的点表示的实数是±$\sqrt{2}$.分析 分析:绝对值的几何定义:数轴上表求数a的点与原点的距离叫做a的绝对值,数轴上离开原点的距离是$\sqrt{2}$就是要求一个实数,使它的绝对值是$\sqrt{2}$.
解答 解:数轴上离开原点的距离是$\sqrt{2}$,说明该实数绝对值是$\sqrt{2}$.
设该点表示的数为x,则|x|=$\sqrt{2}$
∴x=±$\sqrt{2}$
点评 本题是考查绝对值的定义,因此正确理解绝对值的几何意义是解答本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{15}$ | B. | $\sqrt{28}$ | C. | $\sqrt{\frac{1}{6}}$ | D. | $\sqrt{0.5}$ |
12.对于二元一次方程-2x+5y=9,下列说法正确的是( )
| A. | 只有一个解 | B. | 有无数个解 | ||
| C. | 共有两个解 | D. | 任何一对有理数都是它的解 |
4.若二次根式$\sqrt{5-2x}$有意义,则x应满足的条件是( )
| A. | x=$\frac{5}{2}$ | B. | x<$\frac{5}{2}$ | C. | x≥$\frac{5}{2}$ | D. | x≤$\frac{5}{2}$ |
11.下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,…,则第⑥个图形中平行四边形的个数为( )
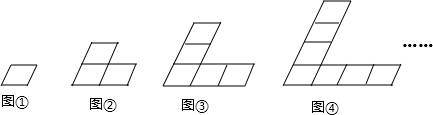

| A. | 45 | B. | 35 | C. | 41 | D. | 65 |
7.要使代数式$\frac{x}{\sqrt{x-3}}$有意义,则x的取值范围是( )
| A. | x=3 | B. | x>3 | C. | x≥3 | D. | x≠0 |