Question

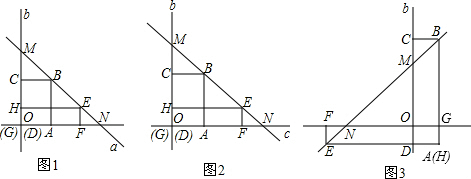
已知直线于O，现将矩形ABCD和矩形EFGH，如图1放置，直线BE分别交直线于.

1.当矩形ABCD≌矩形EFGH时，（如图1） BM与 NE的数量关系是            ；

2.当矩形ABCD与矩形EFGH不全等，但面积相等时，把两矩形如图2，3那样放置，问在这两种放置的情形中，（1）的结论都还成立吗？如果你认为都成立，请你利用图3给予证明，若认为BM与 NE的有不同的数量关系，先分别写出其数量关系式，再证明.

 

Answer 1

 

1.BM= NE

2.如图2，3那样放置（1）中的结论都成立,

证明: 如图3,在矩形ABCD和矩形EFGH中,FN∥EH,,∠FNE=∠BEA,∠EFN=∠A=90°

∴△EFN∽△BAE,同理:△BCM∽△EAB

∴…………①, ………………②

①÷②得,

又∵EF×HE=AB×BC, ∴=1, ∴ EN=BM

解析:略