题目内容
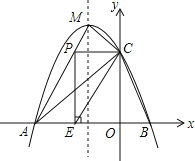
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点
与x轴交于A、B两点,与y轴交于点![]() ,且此抛物线的顶点坐标为
,且此抛物线的顶点坐标为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 设点D为已知抛物线对称轴上的任意一点,当
设点D为已知抛物线对称轴上的任意一点,当![]() 与
与![]() 面积相等时,求点D的坐标;
面积相等时,求点D的坐标;
![]() 点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将
点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将![]() 沿直线CE翻折,使点P的对应点
沿直线CE翻折,使点P的对应点![]() 与P、E、C处在同一平面内,请求出点
与P、E、C处在同一平面内,请求出点![]() 坐标,并判断点
坐标,并判断点![]() 是否在该抛物线上.
是否在该抛物线上.
【答案】![]() 点D的坐标为
点D的坐标为![]() 或
或![]() 点
点![]() 不在该抛物线上
不在该抛物线上
【解析】
![]() 由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;
由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;
![]() 设点D坐标为
设点D坐标为![]() ,根据三角形的面积公式以及
,根据三角形的面积公式以及![]() 与
与![]() 面积相等,即可得出关于
面积相等,即可得出关于![]() 含绝对值符号的一元一次方程,解方程即可得出结论;
含绝对值符号的一元一次方程,解方程即可得出结论;
![]() 作点P关于直线CE的对称点
作点P关于直线CE的对称点![]() ,过点
,过点![]() 作
作![]() 轴于H,设
轴于H,设![]() 交y轴于点
交y轴于点![]() 根据对称的性质即可得出
根据对称的性质即可得出![]() ≌
≌![]() ,从而得出
,从而得出![]() ,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标,在
,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标,在![]() 中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点
中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点![]() 的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.
的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.
![]() 抛物线
抛物线![]() 经过点
经过点![]() ,顶点为
,顶点为![]() ,
,
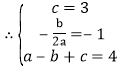 ,解得:
,解得: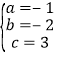 ,
,
![]() 所求抛物线的解析式为
所求抛物线的解析式为![]() ,
,
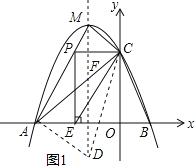
![]() 依照题意画出图形,如图1所示,
依照题意画出图形,如图1所示,
令![]() ,解得:
,解得:![]() 或
或![]() ,
,
故A![]() ,
,![]() ,
,
![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,
设AC交对称轴![]() 于
于![]() ,
,
由点![]() 、
、![]() 可知直线AC的解析式为
可知直线AC的解析式为![]() ,
,
![]() ,即
,即![]() ,
,
设点D坐标为![]() ,
,
则![]() .,
.,
又![]() ,且
,且![]() ,
,
![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() 或
或![]() ;
;
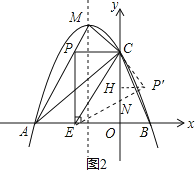
![]() 如图2,点
如图2,点![]() 为点P关于直线CE的对称点,过点
为点P关于直线CE的对称点,过点![]() 作
作![]() 轴于H,设
轴于H,设![]() 交y轴于点N.
交y轴于点N.
在![]() 和
和![]() 中,
中,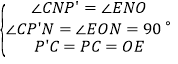 ,
,
![]() ≌
≌![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 、
、![]() 可知直线AM的解析式为
可知直线AM的解析式为![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即点
,即点![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由勾股定理,得:
中,由勾股定理,得:![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() ,
,
由![]() ∽
∽![]() 可得:
可得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,
将点![]() 代入抛物线解析式,
代入抛物线解析式,
得:![]() ,
,
![]() 点
点![]() 不在该抛物线上.
不在该抛物线上.

练习册系列答案
相关题目