题目内容
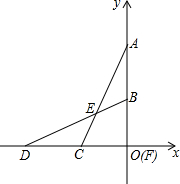 在平面直角坐标系中,将两块全等的含90°角的三角形纸板△ACF与△DBF如图摆放在一起(直角顶点F与原点O重合)
在平面直角坐标系中,将两块全等的含90°角的三角形纸板△ACF与△DBF如图摆放在一起(直角顶点F与原点O重合)(1)求证:AE=DE;
(2)若直线DB的函数关系式为y=
| 1 |
| 2 |
考点:待定系数法求一次函数解析式,全等三角形的性质
专题:
分析:(1)连接AD,根据等腰三角形的性质求得AO=DO,∠OAC=∠ODB,从而求得∠OAD=∠ODA,进而求得∠EAD=∠EDA,根据等角对等边即可证得结论;
(2)根据D、B的坐标得出A、C的坐标,根据待定系数法即可求得直线AC的函数关系式.
(2)根据D、B的坐标得出A、C的坐标,根据待定系数法即可求得直线AC的函数关系式.
解答:解:(1)连接AD,
∵△ACO≌△DBO,
∴AO=DO,∠OAC=∠ODB
∴∠OAD=∠ODA,
又∵∠OAC=∠ODB,
∴∠EAD=∠EDA,
∴AE=DE;
(2)∵直线DB的函数关系式为y=
x+2,
∴D点坐标(-4,0),B点坐标(0,2),
∴OD=4,OB=2,
∵△ACO≌△DBO,
∴AO=OD=4,OC=OB=2,
∴C点坐标(-2,0),A点坐标(0,4),
设直线AC的函数关系式为y=kx+b,
∴
解得
,
∴直线AC的函数关系式为y=2x+4.
∵△ACO≌△DBO,
∴AO=DO,∠OAC=∠ODB
∴∠OAD=∠ODA,
又∵∠OAC=∠ODB,
∴∠EAD=∠EDA,
∴AE=DE;
(2)∵直线DB的函数关系式为y=
| 1 |
| 2 |
∴D点坐标(-4,0),B点坐标(0,2),
∴OD=4,OB=2,
∵△ACO≌△DBO,
∴AO=OD=4,OC=OB=2,
∴C点坐标(-2,0),A点坐标(0,4),
设直线AC的函数关系式为y=kx+b,
∴
|
|
∴直线AC的函数关系式为y=2x+4.
点评:本题考查了待定系数法求一次函数的解析式,三角形全等的性质,等腰三角形的判断和性质等,熟练掌握性质定理以及待定系数法是解题的关键.

练习册系列答案
相关题目
下列四个式子中,是一元一次方程的是( )
| A、x-2y=3 |
| B、3x-6=2x |
| C、x2=1 |
| D、2x=3y |
 如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.
如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.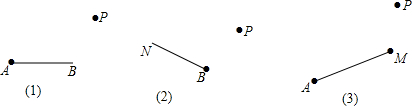
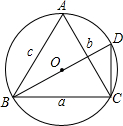 如图,在锐角△ABC中,BC=a,CA=b,AB=c,其外接圆的半径为R.求证:
如图,在锐角△ABC中,BC=a,CA=b,AB=c,其外接圆的半径为R.求证: