题目内容

如图，⊙O1，⊙O2、相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，则弦AB的长为（　　）

　

A．

4.8cm

B．

9.6cm

C．

5.6cm

D．

9.4cm

考点：

相交两圆的性质．

分析：

根据相交两圆的性质得出AC=AB，进而利用勾股定理得出AC的长．

解答：

解：连接AO1，AO2，

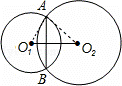
∵⊙O1，⊙O2相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，

∴O1O2⊥AB，

∴AC=AB，

设O1C=x，则O2C=10﹣x，

∴62﹣x2=82﹣（10﹣x）2，

解得：x=3.6，

∴AC2=62﹣x2=36﹣3.62=23.04，

∴AC=4.8cm，

∴弦AB的长为：9.6cm．

故选：B．

点评：

此题考查了相交圆的性质与勾股定理．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与方程思想的应用．

练习册系列答案
相关题目
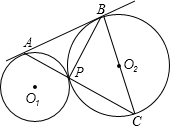精英家教网如图，⊙O1与⊙O2外切于点P，外公切线AB切⊙O1于点A，切⊙O2于点B，
（1）求证：AP⊥BP；
（2）若⊙O1与⊙O2的半径分别为r和R，求证：
AP2
BP2
=
r
R
；
（3）延长AP交⊙O2于C，连接BC，若r：R=2：3，求tan∠C的值．
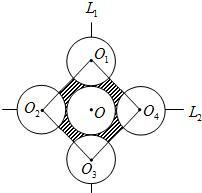精英家教网如图，⊙O1、⊙O2相交于点A、B，现给出4个命题：
（1）若AC是⊙O2的切线且交⊙O1于点C，AD是⊙O1的切线且交⊙O2于点D，则AB2=BC•BD；
（2）连接AB、O1O2，若O1A=15cm，O2A=20cm，AB=24cm，则O1O2=25cm；
（3）若CA是⊙O1的直径，DA是⊙O2的一条非直径的弦，且点D、B不重合，则C、B、D三点不在同一条直线上；
（4）若过点A作⊙O1的切线交⊙O2于点D，直线DB交⊙O1于点C，直线CA交⊙O2于点E，连接DE，则DE2=DB•DC．
则正确命题的序号是
 
．（在横线上填上所有正确命题的序号）
精英家教网如图，⊙O1，⊙O2，⊙O3，⊙O4，⊙O的半径均为2cm，⊙O与⊙O1，⊙O3相外切，⊙O与⊙O2，⊙O4相外切，并且圆心分别位于两条互相垂直的直线L1，L2上，连接O1，O2，O3，O4得四边形O1O2O3O4，则图中阴影部分的面积为
 
cm2．（π≈3.14）
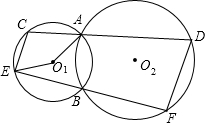精英家教网已知：如图，⊙O1和⊙O2相交于A、B两点，经过A的直线CD与⊙O1交于点C、与⊙O2交于点D，经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F，连接CE、DF．若∠AO1E=100°，则∠D的度数为
 
度．
（1998•南京）如图，⊙O1和⊙O2内切于点P，⊙O2的弦AB经过⊙O1的圆心O1，交⊙O1于点C、D，若AC：CD：BD=3：4：2，则⊙O1与⊙O2的直径之比为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网