题目内容
 如图,直线y=
如图,直线y=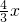 与双曲线y=
与双曲线y= (x>0)交于点A、将直线y=
(x>0)交于点A、将直线y=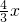 向右平移
向右平移 个单位后,与双曲线y=
个单位后,与双曲线y= (x>0)交于点B,与x轴交于点C,若
(x>0)交于点B,与x轴交于点C,若 ,则k的值为
,则k的值为
- A.2
- B.6
- C.12
- D.8
C
分析:首先表示出直线BC的解析式,根据直线平移的距离,可得C( ,0),然后设出点A的坐标,若AO=2BC,那么A点横、纵坐标分别为B点横、纵坐标的2倍,结合点C的坐标,即可表示出点B的坐标;由于A、B都在双曲线的图象上,那么它们横、纵坐标的积相等,可据此确定点A的坐标,从而求得k的值.
,0),然后设出点A的坐标,若AO=2BC,那么A点横、纵坐标分别为B点横、纵坐标的2倍,结合点C的坐标,即可表示出点B的坐标;由于A、B都在双曲线的图象上,那么它们横、纵坐标的积相等,可据此确定点A的坐标,从而求得k的值.
解答:将直线y=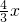 向右平移
向右平移 个单位后得:直线BC:y=
个单位后得:直线BC:y= (x-
(x- )=
)= x-6;
x-6;
设A(x, x),
x), ,则B(
,则B( +
+ ,
, x);
x);
由于A、B都在双曲线的函数图象上,故:
k=x• x=(
x=( +
+ )•
)• x,整理得:
x,整理得:
x2-3x=0,解得x=0(舍去),x=3;
∴A(3,4),k=3×4=12;
故选C.
点评:此题主要考查函数图象的平移以及反比例函数图象上点的坐标意义等知识,难度适中.
分析:首先表示出直线BC的解析式,根据直线平移的距离,可得C(
 ,0),然后设出点A的坐标,若AO=2BC,那么A点横、纵坐标分别为B点横、纵坐标的2倍,结合点C的坐标,即可表示出点B的坐标;由于A、B都在双曲线的图象上,那么它们横、纵坐标的积相等,可据此确定点A的坐标,从而求得k的值.
,0),然后设出点A的坐标,若AO=2BC,那么A点横、纵坐标分别为B点横、纵坐标的2倍,结合点C的坐标,即可表示出点B的坐标;由于A、B都在双曲线的图象上,那么它们横、纵坐标的积相等,可据此确定点A的坐标,从而求得k的值.解答:将直线y=
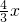 向右平移
向右平移 个单位后得:直线BC:y=
个单位后得:直线BC:y= (x-
(x- )=
)= x-6;
x-6;设A(x,
 x),
x), ,则B(
,则B( +
+ ,
, x);
x);由于A、B都在双曲线的函数图象上,故:
k=x•
 x=(
x=( +
+ )•
)• x,整理得:
x,整理得:x2-3x=0,解得x=0(舍去),x=3;
∴A(3,4),k=3×4=12;
故选C.
点评:此题主要考查函数图象的平移以及反比例函数图象上点的坐标意义等知识,难度适中.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.
如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.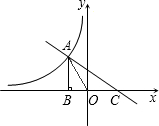 O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2. 如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为
如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为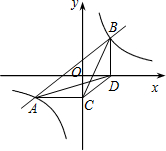 如图,直线AB与双曲线y=
如图,直线AB与双曲线y=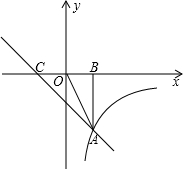 轴于点B,且CO=2BO.
轴于点B,且CO=2BO.