题目内容
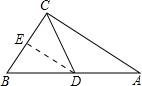
如图所示，在△ABC中，∠ACB=90°．
（1）当点D在斜边AB内部时，求证：
=
．
（2）当点D与点A重合时，第（1）小题中的等式是否存在？请说明理由．
（3）当点D在BA的延长线上时，第（1）小题中的等式是否存在？请说明理由．
（1）当点D在斜边AB内部时，求证：
| CD2-BD2 |
| BC2 |
| AD-BD |
| AB |
（2）当点D与点A重合时，第（1）小题中的等式是否存在？请说明理由．
（3）当点D在BA的延长线上时，第（1）小题中的等式是否存在？请说明理由．
证明：（1）作DE⊥BC，垂足为E．由勾股定理得
所以
=
=
-
．
因为DE∥AC，所以
=
，
=
．
故
=
-
=
．
（2）当点D与点A重合时，第（1）小题中的等式仍然成立．
此时有AD=0，CD=AC，BD=AB．
所以
=
=
=-1，
=
=-1．
从而第（1）小题中的等式成立．
（3）当点D在BA的延长线上时，第（1）小题中的等式不成立．
作DE⊥BC，交BC的延长线于点E，则
而
=
=-1，
所以
≠
．
|
所以
| CD2-BD2 |
| BC2 |
| CE-BE |
| BC |
| CE |
| BC |
| BE |
| BC |
因为DE∥AC，所以
| CE |
| BC |
| AD |
| AB |
| BE |
| BC |
| BD |
| AB |
故
| CD2-BD2 |
| BC2 |
| AD |
| AB |
| BD |
| AB |
| AD-BD |
| AB |
（2）当点D与点A重合时，第（1）小题中的等式仍然成立．
此时有AD=0，CD=AC，BD=AB．
所以
| CD2-BD2 |
| BC2 |
| AC2-AB2 |
| BC2 |
| -BC2 |
| BC2 |
| AD-BD |
| AB |
| -AB |
| AB |
从而第（1）小题中的等式成立．
（3）当点D在BA的延长线上时，第（1）小题中的等式不成立．
作DE⊥BC，交BC的延长线于点E，则
|
而
| AD-BD |
| AB |
| -AB |
| AB |
所以
| CD2-BD2 |
| BC2 |
| AD-BD |
| AB |
练习册系列答案
快乐5加2金卷系列答案
相关题目
