题目内容
7.已知关于x、y的二元一次方程$\left\{\begin{array}{l}{x-y=3a①}\\{x+3y=4-a②}\end{array}\right.$(1)当a=1时,求两方程的公共解;
(2)若$\left\{\begin{array}{l}{x={x}_{0}}\\{y={y}_{0}}\end{array}\right.$是两方程的公共解,x0≤0,求y0的取值范围.
分析 (1)把a=1代入二元一次方程组,求出x、y的值即可;
(2)先用a表示出x0,y0的值,再由x0≤0,即可得出y0的取值范围.
解答 解:(1)∵当a=1时,原方程组可化为$\left\{\begin{array}{l}{x-y=3①}\\{x+3y=3②}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$;
(2)解方程组$\left\{\begin{array}{l}{x-y=3a①}\\{x+3y=4-a②}\end{array}\right.$得,$\left\{\begin{array}{l}{x=1+2a}\\{y=1-a}\end{array}\right.$,
∵$\left\{\begin{array}{l}{x={x}_{0}}\\{y={y}_{0}}\end{array}\right.$是两方程的公共解,
∴$\left\{\begin{array}{l}{{x}_{0}=1+2a}\\{{y}_{0}=1-a}\end{array}\right.$,
∵x0≤0,即1+2a≤0,解得a≤-$\frac{1}{2}$,
∴1-a≥$\frac{3}{2}$,
∴y0≥$\frac{3}{2}$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
相关题目
17.下列结论错误的是( )
| A. | 等边三角形都相似 | B. | 正方形都相似 | ||
| C. | 所有长方形都相似 | D. | 等腰直角三角形都相似 |
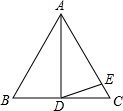 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°.
如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是同位角相等,两直线平行.
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是同位角相等,两直线平行. 要设计一幅长30cm,宽20cm的图案,制成一幅矩形挂图,如图所示,其中有两横两竖的彩条(横竖彩条的宽度相等).如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度?设彩条的宽为x cm,那么x满足的方程为(30-2x)(20-2x)=30×20×(1-$\frac{1}{4}$).
要设计一幅长30cm,宽20cm的图案,制成一幅矩形挂图,如图所示,其中有两横两竖的彩条(横竖彩条的宽度相等).如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度?设彩条的宽为x cm,那么x满足的方程为(30-2x)(20-2x)=30×20×(1-$\frac{1}{4}$).