题目内容
 如图,已知⊙O中,
如图,已知⊙O中, =
= =
= ,OB、OC分别交AC、BD于E、F.求证:△EOF是等腰三角形.
,OB、OC分别交AC、BD于E、F.求证:△EOF是等腰三角形.
证明:∵ =
= =
= ,
,
∴OB⊥AC,OC⊥BD, =
= ,
,
∴OE=OF,
∴△EOF是等腰三角形.
分析:由于 =
= =
= ,根据垂径定理的推论得到OB⊥AC,OC⊥BD,且
,根据垂径定理的推论得到OB⊥AC,OC⊥BD,且 =
= ,即OE和OE为等弦的弦心距,所以OE=OF,由此可判断△EOF是等腰三角形.
,即OE和OE为等弦的弦心距,所以OE=OF,由此可判断△EOF是等腰三角形.
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.
 =
= =
= ,
,∴OB⊥AC,OC⊥BD,
 =
= ,
,∴OE=OF,
∴△EOF是等腰三角形.
分析:由于
 =
= =
= ,根据垂径定理的推论得到OB⊥AC,OC⊥BD,且
,根据垂径定理的推论得到OB⊥AC,OC⊥BD,且 =
= ,即OE和OE为等弦的弦心距,所以OE=OF,由此可判断△EOF是等腰三角形.
,即OE和OE为等弦的弦心距,所以OE=OF,由此可判断△EOF是等腰三角形.点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点. 29、如图,已知△ABC中,AD⊥BC于D,AD=BD,DC=DE.求证:∠C=∠1.
29、如图,已知△ABC中,AD⊥BC于D,AD=BD,DC=DE.求证:∠C=∠1. 34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=
34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC= 如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.
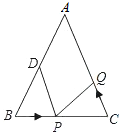
如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2. 如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证:
如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证: