题目内容
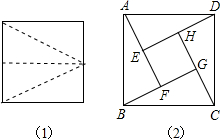将一个面积为7的正方形分割成如图1所示的四个形状相同、大小相等的直角三角形，再将这四个直角三角形拼成如图2所示的正方形ABCD，其中四边形EFGH也是正方形，求正方形ABCD的面积．分析：根据将一个面积为7的正方形分割成四个形状相同、大小相等的直角三角形得出直角三角形斜边长度，进而得出正方形ABCD的面积．
解答：
解：∵将一个面积为7的正方形分割成四个形状相同、大小相等的直角三角形，
∴a=
，b=
，
∴c2=a2+b2=7+
=
，
故正方形ABCD的面积为：
．
解：∵将一个面积为7的正方形分割成四个形状相同、大小相等的直角三角形，∴a=
| 7 |
| ||
| 2 |
∴c2=a2+b2=7+
| 7 |
| 4 |
| 35 |
| 4 |
故正方形ABCD的面积为：
| 35 |
| 4 |
点评：此题主要考查了勾股定理的应用以及正方形的性质，根据已知得出直角三角形斜边长度是解题关键．
练习册系列答案
相关题目
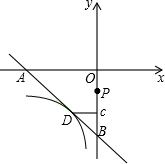
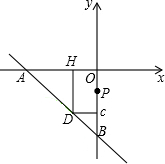
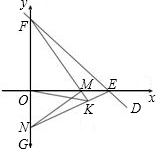
如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为
（2013•恩施州）如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为（ ）
