题目内容
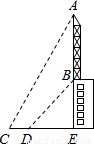
 如图,在点C测得天线AB的顶端A的仰角是60°,从点C向楼底E走6m到达点D,测得天线底端B的仰角是45°,已知天线AB=25m,求楼高BE(用根号表示)
如图,在点C测得天线AB的顶端A的仰角是60°,从点C向楼底E走6m到达点D,测得天线底端B的仰角是45°,已知天线AB=25m,求楼高BE(用根号表示)
分析:首先设楼高BE为xm,由∠BDE=45°,AE⊥CE,即可求得DE=BE=xm,即可求得AE与CE的长,然后由tan∠C=tan60°=
,即可得方程
=
,解此方程即可求得答案.
| AE |
| CE |
| 25+x |
| 6+x |
| 3 |
解答:解:根据题意得:∠C=60°,∠BDE=45°,AE⊥CE,
∴∠E=90°.
设楼高BE为xm.
在Rt△BDE中,DE=
=
=BE=xm,
∴AE=AB+BE=(25+x)m,
CE=CD+DE=(6+x)m,
∴tan∠C=tan60°=
,
∴
=
,
解得:x=
,
∴BE=
m.
∴楼高BE为
m.
∴∠E=90°.
设楼高BE为xm.
在Rt△BDE中,DE=
| BE |
| tan∠BDE |
| BE |
| tan45° |
∴AE=AB+BE=(25+x)m,
CE=CD+DE=(6+x)m,
∴tan∠C=tan60°=
| AE |
| CE |
∴
| 25+x |
| 6+x |
| 3 |
解得:x=
19
| ||
| 2 |
∴BE=
19
| ||
| 2 |
∴楼高BE为
19
| ||
| 2 |
点评:此题考查了仰角的知识.要求学生能借助仰角构造直角三角形并解直角三角形,注意数形结合思想与方程思想应用.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
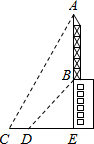 (2005•闸北区二模)已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.
(2005•闸北区二模)已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE. 如图,在点C测得天线AB的顶端A的仰角是60°,从点C向楼底E走6m到达点D,测得天线底端B的仰角是45°,已知天线AB=25m,求楼高BE(用根号表示)
如图,在点C测得天线AB的顶端A的仰角是60°,从点C向楼底E走6m到达点D,测得天线底端B的仰角是45°,已知天线AB=25m,求楼高BE(用根号表示)