Question

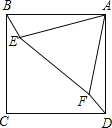
【题目】阅读材料：如图1，中，点，在边上，点在上，，，，延长，交于点，，求证：．

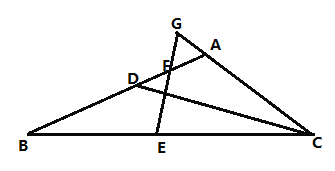
等腰三角形是一种常见的轴对称图形，几何试题中我们常将一腰所在的三角形沿着等腰三角形的对称轴进行翻折，从而构造轴对称图形．

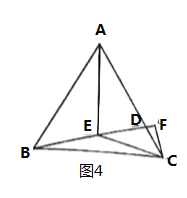
①小明的想法是：将放到中，沿等腰的对称轴进行翻折，即作交于(如图2)

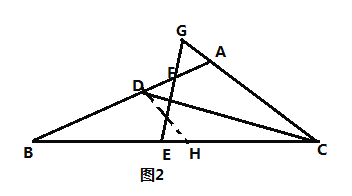
②小白的想法是：将放到中，沿等腰的对称轴进行翻折，即作交的延长线于(如图3)

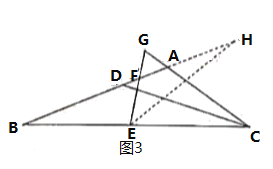
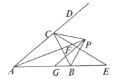
经验拓展：等边中，是上一点，连接，为上一点，，过点作交的延长线于点，，若，，求的长(用含，的式子表示)．

Answer 1

【答案】①证明见解析；②证明见解析；[经验拓展]．

【解析】

阅读材料：①先根据三角形全等的判定定理得出，再根据三角形全等的性质可得，又根据角的和差、等腰三角形的性质得出两组相等的角，然后根据三角形全等的判定定理与性质可得，最后根据等量代换即可得证；

②先根据三角形全等的判定定理得出，再根据三角形全等的性质可得，又根据角的和差、等腰三角形的性质得出两组相等的角，然后根据三角形全等的判定定理与性质可得，即得证；

经验拓展：先根据等腰三角形的性质、邻补角的定义得出，再根据三角形全等的判定定理与性质得出，设，根据等腰三角形的性质、等边三角形的性质分别求出，然后根据角的和差可得，最后根据等腰三角形的判定与性质得出，从而根据线段的和差即可得出答案．

阅读材料：

①小明做法：作交于，则

，

，即

；

②小白做法：作交的延长线于

，即

，即

；

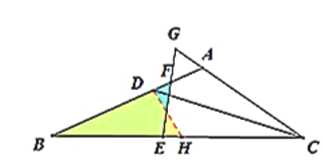
经验拓展：延长至点，使得，连接

是等边三角形，设

是等腰三角形

（等腰三角形的三线合一）

．