题目内容
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
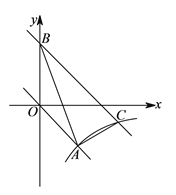
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
【答案】(1)反比例函数表达式为![]() ,正比例函数表达式为
,正比例函数表达式为![]() ;
;
(2)![]() ,
, ![]() .
.
【解析】试题分析:(1)将点A坐标(2,-2)分别代入y=kx、y=![]() 求得k、m的值即可;(2)由题意得平移后直线解析式,即可知点B坐标,联立方程组求解可得第四象限内的交点C得坐标,可将△ABC的面积转化为△OBC的面积.
求得k、m的值即可;(2)由题意得平移后直线解析式,即可知点B坐标,联立方程组求解可得第四象限内的交点C得坐标,可将△ABC的面积转化为△OBC的面积.
试题解析:(![]() )把
)把![]() 代入反比例函数表达式
代入反比例函数表达式![]() ,
,
得![]() ,解得
,解得![]() ,
,
∴反比例函数表达式为![]() ,
,
把![]() 代入正比例函数
代入正比例函数![]() ,
,
得![]() ,解得
,解得![]() ,
,
∴正比例函数表达式为![]() .
.
(![]() )直线
)直线![]() 由直线
由直线![]() 向上平移
向上平移![]() 个单位所得,
个单位所得,
∴直线![]() 的表达式为
的表达式为![]() ,
,
由 ,解得
,解得![]() 或
或![]() ,
,
∵![]() 在第四象限,
在第四象限,
∴![]() ,
,
连接![]() ,
,
∵![]() ,
,

![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目