Question

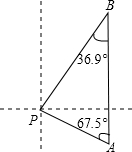如图某天上午9时，向阳号轮船位于A处，观测到某港口城市P位于轮船的北偏西67.5°，轮船以21海里/时的速度向正北方向行驶，下午2时该船到达B处，这时观测到城市P位于该船的南偏西36.9°方向，求此时轮船所处位置B与城市P的距离？
（）

Answer 1

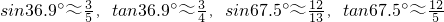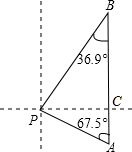解：如图：根据题意得：PC⊥AB，
设PC=x海里．
在Rt△APC中，∵tan∠A=，
∴AC==，
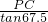在Rt△PCB中，∵tan∠B=，
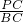∴BC==，
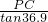∵AC+BC=AB=21×5，
∴+=21×5，
解得：x=60，
∴PC=60海里，
∵sin∠B=，
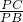∴PB=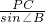==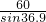60×=100（海里）．
∴向阳号轮船所处位置B与城市P的距离为100海里．
分析：首先根据题意可得PC⊥AB，然后设PC=x海里，分别在Rt△APC中与Rt△PCB中，利用正切函数求得出AC与BC的长，由AB=21×5，即可得方程，解此方程即可求得x的值，继而求得答案．
点评：此题考查了方向角问题．此题难度适中，注意结合实际问题，利用解直角三角形的相关知识求解是解此题的关键，注意数形结合思想的应用．