题目内容
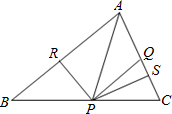 25、如图:△ABC中AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S.判断PQ与AB位置关系并证明.
25、如图:△ABC中AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S.判断PQ与AB位置关系并证明.分析:首先由PR⊥AB,PS⊥AC,PR=PS得∠BAP=∠PAC,再由AQ=PQ得∴∠PAC=∠QPA,从而得∠BAP=∠QPA,所以得出断PQ与AB位置关系平行.
解答:解:PQ∥AB,
证明:∵PR⊥AB,PS⊥AC,PR=PS
∴∠BAP=∠PAC
∵AQ=PQ
∴∠PAC=∠QPA
∴∠BAP=∠QPA
∴PQ∥AB.
证明:∵PR⊥AB,PS⊥AC,PR=PS
∴∠BAP=∠PAC
∵AQ=PQ
∴∠PAC=∠QPA
∴∠BAP=∠QPA
∴PQ∥AB.
点评:此题考查的知识点是平行线的判定,关键是运用直角三角形斜边和直角边对应相等三角形全等及等腰三角形的性质得出结论.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
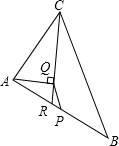 已知:如图,△ABC中,∠A>∠B,CR是∠ACB的平分线且交AB于R,AQ⊥CR,垂足为Q,P为AB的中点,求证:PQ=
已知:如图,△ABC中,∠A>∠B,CR是∠ACB的平分线且交AB于R,AQ⊥CR,垂足为Q,P为AB的中点,求证:PQ= 以点P为圆心,PA为半径画⊙P交AC于点Q.
以点P为圆心,PA为半径画⊙P交AC于点Q. 如图,△ABC中,PN⊥AB于N,PM⊥AC于M,PN=PM,PQ∥AB,则下列结论:①AM=AN;②AQ=PQ;③∠NAP=∠MAP,其中正确的是( )
如图,△ABC中,PN⊥AB于N,PM⊥AC于M,PN=PM,PQ∥AB,则下列结论:①AM=AN;②AQ=PQ;③∠NAP=∠MAP,其中正确的是( )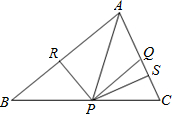 如图:△ABC中AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S.判断PQ与AB位置关系并证明.
如图:△ABC中AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S.判断PQ与AB位置关系并证明.