Question

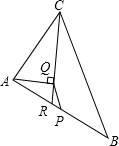已知：如图，△ABC中，∠A＞∠B，CR是∠ACB的平分线且交AB于R，AQ⊥CR，垂足为Q，P为AB的中点，求证：PQ=

1

2

（BC-AC）．

Answer 1

分析：本题可通过构建全等三角形来实现线段之间的转换．
延长AQ与BC交于D．
根据∠ACQ=∠DCQ，CQ⊥AD，AC=CD，我们可得出△ACQ≌△DCQ．
那么AQ=QD，AC=CD． BC-AC=BC-CD=BD．那么只要证明BD=2PQ即可．
根据AQ=QD，P是AB中点，那么PQ就是三角形ABD的中位线，于是就得出了BD=2PQ，也就能求出所要证明的条件了．

解答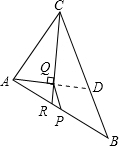：解：延长AQ与BC交于D．
∵CR是∠ACB的平分线，
∴∠ACQ=∠DCQ．
∵∠AQC=∠DQC=90°，CQ=CQ，
∴△ACQ≌△DCQ．（ASA）
∴AQ=QD，AC=CD，
∴BC-CD=BC-AC=BD．
∵P是AB的中点，且AQ=QD，
∴PQ是三角形ABD的中位线．
∴PQ=

1

2

BD．
∴PQ=

1

2

（BC-AC）．

点评：本题主要考查了全等三角形的判定，本题中通过构建全等三角形来实现线段之间的转换是解题的关键．