题目内容
如图,⊙O直径AB上一点P,AB=2,∠BAC=20°,D是弧BC中点,则PD+PC的最小值为

A.1 B. C.
C. D.
D.
B.
【解析】
试题分析:作D点关于AB的对称点E,连CE交AB于P点,连OE,如图,

∴弧DC=弧BD=弧BE,它们的圆心角为20°,
∴∠COE=60°
∴CE是PD+PC的最小值.
又∵OC=OE,
∴△COE为等边三角形.
∴CE=OC=OD=1,
∴PD+PC的最小值为1.
故选B.
考点:1.垂径定理;2.勾股定理;3.轴对称-最短路线问题.

练习册系列答案
相关题目
(7分)下表给出了某班6名同学身高情况(单位:cm)
学 生 | A | B | C | D | E | F |
身高(单位:cm) | 165 |
| 166 |
|
| 172 |
身高与班级平均身高的差值 |
| +2 |
|
| +4 |
|
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6个同学身高的达标率是多少?(精确到小数点后两位)

 的解是 .
的解是 .
 有两个不相等的实数根,那么
有两个不相等的实数根,那么 的取值范围是
的取值范围是 >
> B.
B. 且
且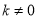
 D.
D. ≥
≥ 且
且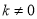
 ,把△EFO缩小,则点E的对应点E′的坐标是( )
,把△EFO缩小,则点E的对应点E′的坐标是( ) 1
1 3
3