题目内容
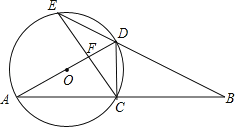
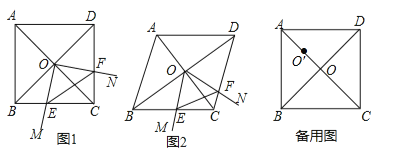
【题目】如图，15个形状大小完全相同的菱形组成网格，菱形的顶点称为格点. 已知菱形的一个角为60°，A、B、C都在格点上，点D在过A、B、C三点的圆弧上，若E也在格点上，且∠AED=∠ACD，则cos∠AEC=________.
【答案】
【解析】将圆补充完整，利用圆周角定理找出点E的位置，再根据菱形的性质即可得出△CME为等边三角形，进而即可得出cos∠AEC的值.
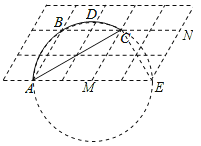
解：将圆补充完整，找出点E的位置，如图所示.
∵
所对的圆周角为∠ACD、∠AEC，
∴图中所标点E符合题意.
∵四边形∠CMEN为菱形，且∠CME=60°，
∴△CME为等边三角形，
∴cos∠AEC=cos60°=
.
故答案为： 
“点睛”本题考查了菱形的性质、等边三角形判定依据圆周角定理，根据圆周角定理结合图形找出点E的位置是解题的关键.
练习册系列答案
相关题目
【题目】在画二次函数
的图象时，甲写错了一次项的系数，列表如下
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 3 | 2 | 3 | 6 | …… |
乙写错了常数项，列表如下：
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | ﹣2 | ﹣1 | 2 | 7 | 14 | …… |
通过上述信息，解决以下问题：
(1)求原二次函数的表达式；
(2)对于二次函数，当
_____时，
的值随的值增大而增大；
(3)若关于的方程
有两个不相等的实数根，求
的取值范围．
