Question

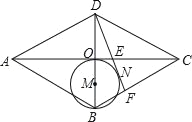
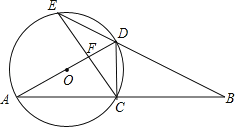
【题目】如图，以AD为直径的⊙O交AB于C点，BD的延长线交⊙O于E点，连CE交AD于F点，若AC＝BC．

（1）求证：；

（2）若，求tan∠CED的值．

Answer 1

【答案】（1）见解析；（2）tan∠CED＝

【解析】

（1）欲证明，只要证明即可；

（2）由，可得，设FO＝2a，OC＝3a，则DF＝a，DE＝1.5a，AD＝DB＝6a，由，可得BDBE＝BCBA，设AC＝BC＝x，则有，由此求出AC、CD即可解决问题.

（1）证明：如下图，连接AE，

∵AD是直径，

∴，

∴DC⊥AB，

∵AC＝CB，

∴DA＝DB，

∴∠CDA＝∠CDB，

∵，，

∴∠BDC＝∠EAC，

∵∠AEC＝∠ADC，

∴∠EAC＝∠AEC，

∴；

（2）解：如下图，连接OC，

∵AO＝OD，AC＝CB，

∴OC∥BD，

∴，

∴，

设FO＝2a，OC＝3a，则DF＝a，DE＝1.5a，AD＝DB＝6a，

∵∠BAD＝∠BEC，∠B＝∠B，

∴，

∴BDBE＝BCBA，设AC＝BC＝x，

则有，

∴，

∴，

∴，

∴.