题目内容
 如图,已知动点A在函数y=
如图,已知动点A在函数y=| 4 |
| x |
(1)当AC=a时,请用含a的代数式表示阴影部分的面积;
(2)若ED:DP=3:5,求阴影部分的面积;
(3)若QE:DP=3:5,求阴影部分的面积.
考点:反比例函数综合题
专题:
分析:(1)四边形AEGC和ABFD都是正方形,△ACE和△ABD都是等腰直角三角形,求得A的纵坐标,然后利用三角形的面积公式即可求解;
(2)作DF⊥x轴于点F,则△AED∽△FDP,则
=
=
=
,然后利用反比例函数中比例系数k的几何意义,即可得到AC•AB=4,即可求解;
(3)设EG=3t,则PF=5t,然后根据△ADE∽△FPD,据此即可得到关于t的方程,求得t的值,进而求解.
(2)作DF⊥x轴于点F,则△AED∽△FDP,则
| AC |
| AB |
| AE |
| DF |
| ED |
| DP |
| 3 |
| 5 |
(3)设EG=3t,则PF=5t,然后根据△ADE∽△FPD,据此即可得到关于t的方程,求得t的值,进而求解.
解答: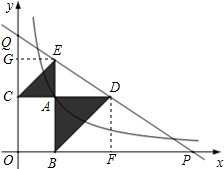 解:(1)在y=
解:(1)在y=
中,令x=a,则y=
,
则S△ACE=
a2,S△ABD=
•(
)2=
,
则阴影部分的面积是:
a2+
;
(2)作DF⊥x轴于点F,则△AED∽△FDP,
则
=
=
,
∵四边形AEGC和ABFD都是正方形,
∴
=
=
=
,
设AC=3x,则AB=5x,
∵反比例的函数的解析式是y=
,
∴AC•AB=4,
∴3x•5x=4,
解得:x2=
,
则阴影部分的面积是:
AC2+
=
×
×9+
=
;
(3):∵QE:DP=3:5,
∴EG:PF=3:5,
设EG=3t,则PF=5t,
∴A(3t,
),
由AC=AE AD=AB,
∴AE=3t,AD=
,DF=
,PF=5t,
∵△ADE∽△FPD,
∴AE:DF=AD:PF,
3t:
=
:5t,即t2=
,
图中阴影部分的面积=
×3t×3t+
×
×
=
.
 解:(1)在y=
解:(1)在y=| 4 |
| x |
| 4 |
| a |
则S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| a |
| 8 |
| a2 |
则阴影部分的面积是:
| 1 |
| 2 |
| 8 |
| a2 |
(2)作DF⊥x轴于点F,则△AED∽△FDP,
则
| AE |
| DF |
| ED |
| DP |
| 3 |
| 5 |
∵四边形AEGC和ABFD都是正方形,
∴
| AC |
| AB |
| AE |
| DF |
| ED |
| DP |
| 3 |
| 5 |
设AC=3x,则AB=5x,
∵反比例的函数的解析式是y=
| 4 |
| x |
∴AC•AB=4,
∴3x•5x=4,
解得:x2=
| 4 |
| 15 |
则阴影部分的面积是:
| 1 |
| 2 |
| 8 |
| AC2 |
| 1 |
| 2 |
| 4 |
| 15 |
| 8 | ||
9×
|
| 68 |
| 15 |
(3):∵QE:DP=3:5,
∴EG:PF=3:5,
设EG=3t,则PF=5t,
∴A(3t,
| 4 |
| 3t |
由AC=AE AD=AB,
∴AE=3t,AD=
| 4 |
| 3t |
| 4 |
| 3t |
∵△ADE∽△FPD,
∴AE:DF=AD:PF,
3t:
| 4 |
| 3t |
| 4 |
| 3t |
4
| ||
| 45 |
图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3t |
| 4 |
| 3t |
13
| ||
| 15 |
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了相似三角形的判定与性质.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
下列说法错误的是( )
| A、任何数的绝对值都不是负数 |
| B、负数的绝对值一定比它本身大 |
| C、任何数的绝对值的相反数都不是正数 |
| D、如果两个数的绝对值相等,那么这两个数也相等 |
若(m+1)xm(m+2)-1+2mx-1=0是关于x的一元二次方程,则m的值是( )
| A、-3 | B、1或-1 |
| C、-3或1 | D、-1 |
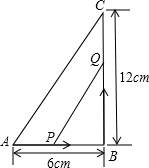 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,Q从点B开始沿BC边向C点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,Q从点B开始沿BC边向C点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?