题目内容
3.已知二次函数y=x2+bx+c经过(1,3),(4,0).(1)求该抛物线的解析式;
(2)求该抛物线与x轴的交点坐标.
分析 (1)把点(1,3),(4,0)代入y=x2+bx+c,求出b和c的值即可求出抛物线的解析式;
(2)设y=0,解关于x的一元二次方程即可求出该抛物线与x轴的交点坐标.
解答 解:(1)依题意把(1,3),(4,0)代入y=x2+bx+c,
得 $\left\{\begin{array}{l}{3=1+b+c}\\{0=16+4b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-6}\\{c=8}\end{array}\right.$,
所以y=x2-6x+8;
(2)设x2-6x+8=0,
解得x1=2,x2=4,
所以该抛物线与x轴的交点坐标为(2,0),(4,0).
点评 本题考查抛物线与x轴的交点,用待定系数法求二次函数的解析式,解题的关键是明确题意,会熟练的求出一元二次的根.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
13.下列各式中结果为正数的是( )
| A. | -(-3) | B. | -|-3| | C. | -23 | D. | (-3)3 |
14.二次函数y=x2+4x-5的图象的对称轴为( )
| A. | x=-4 | B. | x=4 | C. | x=-2 | D. | x=2 |
12.若等腰三角形的两边长分别为4和6,则它的周长是( )
| A. | 14 | B. | 15 | C. | 16 | D. | 14或16 |
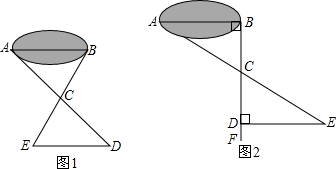 八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案: 如图,是2016年11月月历:
如图,是2016年11月月历: