题目内容
6.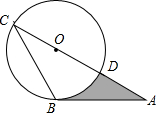 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
分析 首先求出∠AOB,OB,然后利用S阴=S△ABO-S扇形OBD计算即可.
解答 解:连接 OB.
OB.
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在Rt△ABO中,∵∠ABO=90°,AB=$\sqrt{3}$,∠A=30°,
∴OB=1,
∴S阴=S△ABO-S扇形OBD=$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{60π•{1}^{2}}{360}$=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
故答案为=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
点评 本题考查切线的性质、等腰三角形的性质、勾股定理,直角三角形30度角性质,解题的关键是学会分割法求面积,记住扇形面积公式,属于中考常考题型.

练习册系列答案
相关题目
18.高速路上因赶时间超速而频频发生交通事故,这样给自己和他人的生命安全带来直接影响,为了解车速情况,一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下:
则这6辆车车速的众数和中位数(单位:千米/时)分别是( )
| 车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 车速(千米/时) | 100 | 95 | 106 | 100 | 120 | 100 |
| A. | 100,95 | B. | 100,100 | C. | 102,100 | D. | 100,103 |
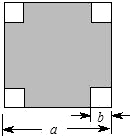 如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.
如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.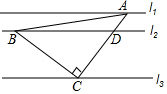 已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,
已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,