题目内容
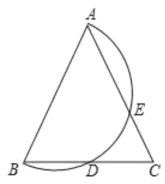
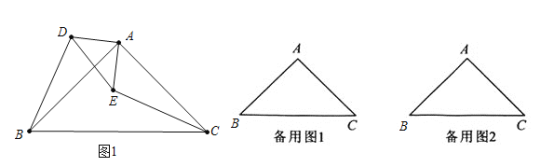
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A旋转.
绕点A旋转.
![]() 当
当![]() 时,求PB的长;
时,求PB的长;
![]() 直接写出旋转过程中线段PB长的最大值与最小值.
直接写出旋转过程中线段PB长的最大值与最小值.
【答案】(1)详见解析;(2)①![]() 或
或![]() ;②PB长的最小值是
;②PB长的最小值是![]() ,最大值是
,最大值是![]() .
.
【解析】
![]() 欲证明
欲证明![]() ,只要证明
,只要证明![]() ≌
≌![]() 即可.
即可.
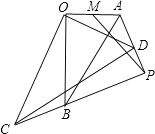
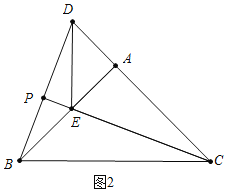
![]() 分两种情形a、如图2中,当点E在AB上时,
分两种情形a、如图2中,当点E在AB上时,![]() 由
由![]() ∽
∽![]() ,得
,得![]() ,由此即可解决问题.
,由此即可解决问题.
b、如图3中,当点E在BA延长线上时,![]() 解法类似.
解法类似.
![]() 、如图4中,以A为圆心AD为半径画圆,当CE在
、如图4中,以A为圆心AD为半径画圆,当CE在![]() 下方与
下方与![]() 相切时,PB的值最小.
相切时,PB的值最小.
b、如图5中,以A为圆心AD为半径画圆,当CE在![]() 上方与
上方与![]() 相切时,PB的值最大.分别求出PB即可.
相切时,PB的值最大.分别求出PB即可.
![]() 证明:如图1中,
证明:如图1中,
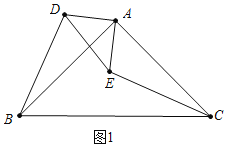
![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
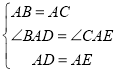 ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() 解:
解:![]() 、如图2中,当点E在AB上时,
、如图2中,当点E在AB上时,![]() .
.
![]() ,
,
![]()
同![]() 可证
可证![]() ≌
≌![]() .
.
![]() .
.
![]() ,
,
![]() ∽
∽![]() .
.
![]()
![]()
![]()
b、如图3中,当点E在BA延长线上时,![]() .
.
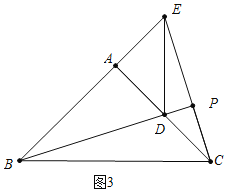
![]() ,
,
![]() ,
,
同![]() 可证
可证![]() ≌
≌![]() .
.
![]() .
.
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上,![]() 或
或![]() .
.
![]() 、如图4中,以A为圆心AD为半径画圆,当CE在
、如图4中,以A为圆心AD为半径画圆,当CE在![]() 下方与
下方与![]() 相切时,PB的值最小.
相切时,PB的值最小.
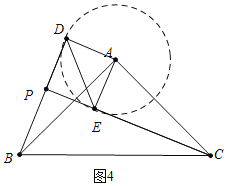
理由:此时![]() 最小,因此PB最小,
最小,因此PB最小,![]() 是直角三角形,斜边BC为定值,
是直角三角形,斜边BC为定值,![]() 最小,因此PB最小
最小,因此PB最小![]()
![]() ,
,
![]() ,
,
由![]() 可知,
可知,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形AEPD是矩形,
四边形AEPD是矩形,
![]() ,
,
![]() .
.
b、如图5中,以A为圆心AD为半径画圆,当CE在![]() 上方与
上方与![]() 相切时,PB的值最大.
相切时,PB的值最大.
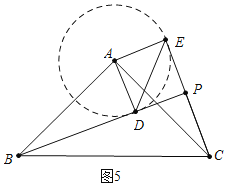
理由:此时![]() 最大,因此PB最大,
最大,因此PB最大,![]() 是直角三角形,斜边BC为定值,
是直角三角形,斜边BC为定值,![]() 最大,因此PB最大
最大,因此PB最大![]()
![]() ,
,
![]() ,
,
由![]() 可知,
可知,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形AEPD是矩形,
四边形AEPD是矩形,
![]() ,
,
![]() .
.
综上所述,PB长的最小值是![]() ,最大值是
,最大值是![]() .
.

练习册系列答案
相关题目