��Ŀ����
����Ŀ����֪ƽ��ͼ��![]() ����
����![]() ��
��![]() ��
��![]() ���������㣬���ǰ��߶�
���������㣬���ǰ��߶�![]() �ij��ȵ����ֵ��Ϊƽ��ͼ��
�ij��ȵ����ֵ��Ϊƽ��ͼ��![]() �ġ����ࡱ�����磬�����εĿ���������ĶԽ��ߵij��ȣ�
�ġ����ࡱ�����磬�����εĿ���������ĶԽ��ߵij��ȣ�
��1��д������ͼ�εĿ��ࣺ
�ٰ뾶Ϊ![]() ��Բ��________��
��Բ��________��
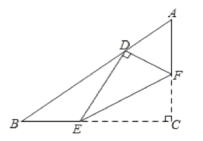
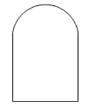
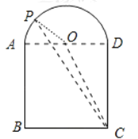
����ͼ���Ϸ��ǰ뾶Ϊ![]() �İ�Բ���·��������ε������ߵġ������Ρ���________��
�İ�Բ���·��������ε������ߵġ������Ρ���________��
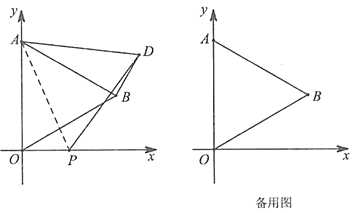
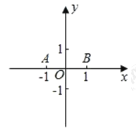
��2����ͼ����ƽ��ֱ������ϵ�У���֪��![]() ��
��![]() ��
��![]() ������ƽ���ڵĵ㣬����
������ƽ���ڵĵ㣬����![]() ��
��![]() ��
��![]() ���γɵ�ͼ��Ϊ
���γɵ�ͼ��Ϊ![]() ����
����![]() �Ŀ���Ϊ
�Ŀ���Ϊ![]() ��
��
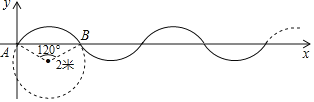
����![]() ����ֱ�ߺ�Բ�滭����
����ֱ�ߺ�Բ�滭����![]() ���ڵ����������������������������Ӱ��ʾ����
���ڵ����������������������������Ӱ��ʾ����
������![]() �ڡ�
�ڡ�![]() ���˶�����
���˶�����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��Բ��
��Բ��![]() �ڹ���
�ڹ���![]() ����
����![]() �ᴹֱ��ֱ���ϣ����ڡ�
�ᴹֱ��ֱ���ϣ����ڡ�![]() �������
�������![]() ������
������![]() ��ֱ��д��Բ��
��ֱ��д��Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1����1����![]() ����2�������Ϊ2���ڵ�
����2�������Ϊ2���ڵ�![]() �ĺ�����ķ�ΧΪ
�ĺ�����ķ�ΧΪ![]() ��
��
��������
��1����ƽ��ͼ��![]() �ġ����ࡱ�Ķ��弴�ɽ�����⣮
�ġ����ࡱ�Ķ��弴�ɽ�����⣮
����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() �����Բ��Բ��Ϊ
�����Բ��Բ��Ϊ![]() ����
����![]() �ǡ�
�ǡ�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() �����
�����![]() �����ֵ���ɽ�����⣮
�����ֵ���ɽ�����⣮
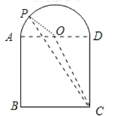
��2������ͼ2��1�У���![]() ���ڵ�������ͼ��������
���ڵ�������ͼ��������![]() �����Ϊ
�����Ϊ![]() ��
��
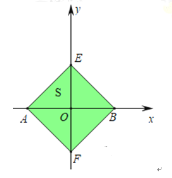
����ͼ2��2�У�����![]() ��
��![]() ����Ҳ�ʱ������
����Ҳ�ʱ������![]() ����
����![]() ����
����![]() �����
�����![]() ��
��![]() ʱ����
ʱ����![]() �����꣬�����жϣ��ٸ��ݶԳ��������
�����꣬�����жϣ��ٸ��ݶԳ��������![]() ��
��![]() ���������μ��ɣ�
���������μ��ɣ�
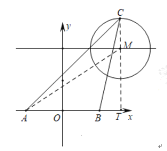
��1���ٰ뾶Ϊ![]() ��Բ�Ŀ�����Ϊ
��Բ�Ŀ�����Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() �����Բ��Բ��Ϊ
�����Բ��Բ��Ϊ![]() ����
����![]() �ǡ�
�ǡ�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() ��
��
��![]() ��
�У�![]()
![]()
![]() ��
��
![]()
![]() ��
��
![]() ����������Ρ��Ŀ���Ϊ
����������Ρ��Ŀ���Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2������ͼ����![]() ���ڵ�������ͼ��������
���ڵ�������ͼ��������![]() �����Ϊ2��
�����Ϊ2��
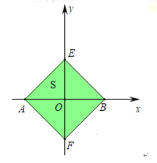
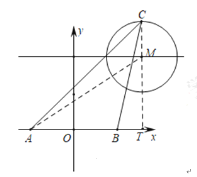
����ͼ������![]() ��
��![]() ����Ҳ�ʱ������
����Ҳ�ʱ������![]() ����
����![]() ����
����![]() ��
��
![]()
![]() ����
����![]()
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]()
![]() ����ʱ
����ʱ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]()
![]() ����ʱ
����ʱ![]() ��
��
![]() ���������ĵ�
���������ĵ�![]() �ĺ�����ķ�ΧΪ
�ĺ�����ķ�ΧΪ![]() ��
��