题目内容
已知三角形两边的长分别是4和3，第三边的长是一元二次方程x2-8x+15=0的一个实数根，则该三角形的面积是（ ）
| A、6 | ||
| B、12 | ||
C、6或2
| ||
D、12或2
|
考点：一元二次方程的应用
专题：
分析：先用因式分解法解一元二次方程，再由三角形的形状分别求出三角形的面积．
解答：
解：∵x2-8x+15=0，
∴（x-5）（x-3）=0，
∴x1=3，x2=5．
当x1=3时，与另两边组成等腰三角形，可求得底边4上的高AD=
，
所以该三角形的面积是4×
÷2=2
；
当x2=5时，与另两边组成直角三角形，
即3，4，5符合直角三角形，
∴该三角形的面积=3×4÷2=6．
综上所述，该三角形的面积是2
或6．
故选：C．
解：∵x2-8x+15=0，∴（x-5）（x-3）=0，
∴x1=3，x2=5．
当x1=3时，与另两边组成等腰三角形，可求得底边4上的高AD=
| 5 |
所以该三角形的面积是4×
| 5 |
| 5 |
当x2=5时，与另两边组成直角三角形，
即3，4，5符合直角三角形，
∴该三角形的面积=3×4÷2=6．
综上所述，该三角形的面积是2
| 5 |
故选：C．
点评：此题主要考查了一元二次方程的解法以及勾股定理和等腰三角形的性质等知识，综合性比较强，结合等腰三角形的面积和直角三角形的判定得出答案是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列计算正确的是（ ）
| A、3a+2b=5ab |
| B、5y-3y=2 |
| C、7a+a=7a2 |
| D、3x2y-2yx2=x2y |
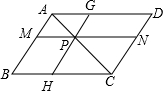如图，?ABCD的对角线AC上有一点P，过P点作HG∥AB，过P点作MN∥AD，图中面积相等的平行四边形有几对？（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
在△ABC中，∠A=150°，AB=2，AC=4，则tanB的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
2013年4月20日，四川雅安市发生7.0级强烈地震．地震无情人有情，社会各阶层人士纷纷伸出援助之手．据不完全统计，仅两天时间就收到捐款捐物总额达9182万元．用科学记数法表示9182万为（ ）
| A、0.9182×108 |
| B、9.182×107 |
| C、9.182×106 |
| D、91.82×106 |
下列运算正确的是（ ）
| A、-x2•x3=-x6 | ||
| B、（a-b）2=a2-2ab+b2 | ||
| C、（a2+b2）2=a4+b4 | ||
D、
|
若A（-2，b）、B（-3，c）是函数y=-x的图象上的两点，则b与c的大小关系为（ ）
| A、b＜c | B、b＞c |
| C、b=c | D、无法判断 |