题目内容
 在正方形ABCD中,连接对角线BD,若BE平分∠CBD,交CD于点E,且CE=3,则AD=
在正方形ABCD中,连接对角线BD,若BE平分∠CBD,交CD于点E,且CE=3,则AD=考点:正方形的性质,角平分线的性质,等腰直角三角形
专题:
分析:正方形的各边相等,因而求AD可以转化为求CD,根据三角形的角平分线的性质定理,就可以求解.
解答: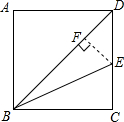 解:过点E作EF⊥BD于F,
解:过点E作EF⊥BD于F,
∵四边形ABCD是正方形,
∴∠CDF=45°,∠C=90°,
∴△BCD是等腰直角三角形,
∵BE平分∠DBC交DC于E,CE=3,
∴EF=CE=3,
∴EF=DF=3,
∴DE=
=3
,
∴CD=DE+CE=3
+3,
即AD=3
+3.
故答案为:3
+3.
 解:过点E作EF⊥BD于F,
解:过点E作EF⊥BD于F,∵四边形ABCD是正方形,
∴∠CDF=45°,∠C=90°,
∴△BCD是等腰直角三角形,
∵BE平分∠DBC交DC于E,CE=3,
∴EF=CE=3,
∴EF=DF=3,
∴DE=
| EF2+DF2 |
| 2 |
∴CD=DE+CE=3
| 2 |
即AD=3
| 2 |
故答案为:3
| 2 |
点评:此题考查正方形的性质,角平分线的性质,以及等腰三角形的性质,注意辅助线的作法.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
若x>y,则下列不等式成立的是( )
A、
| ||||
| B、x>y-1 | ||||
| C、-2x>-2y | ||||
| D、x-3<y-3 |
 如图,直线AB、CD相交于点O,∠1=40°,求∠2,∠3,∠4的度数.
如图,直线AB、CD相交于点O,∠1=40°,求∠2,∠3,∠4的度数. 如图四边形ABCD是边长为1的正方形,△BPC是等边三角形,则△BPD的面积为
如图四边形ABCD是边长为1的正方形,△BPC是等边三角形,则△BPD的面积为 如图,请你添加一个条件,使得AB∥DE,你添加的条件是
如图,请你添加一个条件,使得AB∥DE,你添加的条件是