题目内容
 将直角三角板ABC绕直角顶点C逆时针旋转角度α,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角α的值为
将直角三角板ABC绕直角顶点C逆时针旋转角度α,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角α的值为考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得∠BCE=α,CB=CE,再利用三角形内角和得到∠CBE=∠CEB=90°-
α,则∠EBF=∠CBE-∠CBA=60°-
α,接着利用三角形外角性质得∠BFE=30°+α,
然后分类讨论:当∠BFE=∠BEF时,即30°+α=60°-
α或当∠BFE=∠BEF时,即30°+α=90°-
α,再分别解方程求出α即可.
| 1 |
| 2 |
| 1 |
| 2 |
然后分类讨论:当∠BFE=∠BEF时,即30°+α=60°-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵直角三角板ABC绕直角顶点C逆时针旋转角度α,得到△DCE,
∴∠BCE=α,CB=CE,
∴∠CBE=∠CEB=
(180°-α)=90°-
α,
∴∠EBF=∠CBE-∠CBA=90°-
α-30°=60°-
α,
∵∠BFE=∠FCB+∠FBC,
∴∠BFE=30°+α,
∵△BEF为等腰三角形,
∴当∠BFE=∠BEF时,即30°+α=60°-
α,解得α=20°;
当∠BFE=∠BEF时,即30°+α=90°-
α,解得α=40°,
即旋转角α的值为20°或40°.
故答案为20°或40°.
∴∠BCE=α,CB=CE,
∴∠CBE=∠CEB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EBF=∠CBE-∠CBA=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFE=∠FCB+∠FBC,
∴∠BFE=30°+α,
∵△BEF为等腰三角形,
∴当∠BFE=∠BEF时,即30°+α=60°-
| 1 |
| 2 |
当∠BFE=∠BEF时,即30°+α=90°-
| 1 |
| 2 |
即旋转角α的值为20°或40°.
故答案为20°或40°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
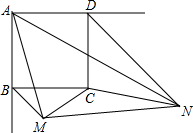 已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.
已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN. 如图,△ABD和△CBD都是等边三角形,点E从A出发向D运动(但不与点A、D重合),同时点F以相同的速度从D出发向C运动(但不与点D、C重合).
如图,△ABD和△CBD都是等边三角形,点E从A出发向D运动(但不与点A、D重合),同时点F以相同的速度从D出发向C运动(但不与点D、C重合). 问题:如图1,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,切点分别是D、E、F,若三角形三边长分别记为BC=a,AC=b,AB=c,内切圆半径记为r,现有小尧和小淇对半径进行计算.下面是两位同学简要的解答过程:
问题:如图1,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,切点分别是D、E、F,若三角形三边长分别记为BC=a,AC=b,AB=c,内切圆半径记为r,现有小尧和小淇对半径进行计算.下面是两位同学简要的解答过程: